
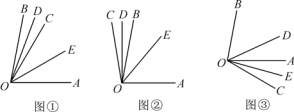
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
【答案】(1) 40°;(2) 40°.
【解析】
(1)利用角平分线定义,得出∠DOE=![]() ∠BOC+
∠BOC+![]() ∠AOC,然后根据∠AOB=80°即可求出∠DOE的度数;
∠AOC,然后根据∠AOB=80°即可求出∠DOE的度数;
(2)∠DOE的大小与(1)中答案相同,仍为40°.由角平分线的定义及角的和差即可得出结论.
(1)∵OD、OE分别是∠BOC和∠COA的平分线,∴∠COD=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,∴∠DOE=∠COD+∠COE=
∠AOC,∴∠DOE=∠COD+∠COE=![]() ∠BOC+
∠BOC+![]() ∠AOC=
∠AOC=![]() ∠AOB=40°;
∠AOB=40°;
(2)∠DOE的大小与(1)中答案相同,仍为40°.选图②说明:∠DOE=∠COE-∠COD=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB=
∠AOB=![]() ×80°=40°.
×80°=40°.


科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



查看答案和解析>>
科目:初中数学 来源: 题型:
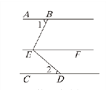
【题目】如图,AB∥CD∥EF,∠1=75,∠2=45,点 G为∠BED 内一点,且 EG把∠BED分成 1 ∶ 2 两部分,则∠GEF 的度数为 ___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
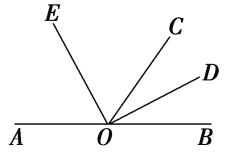
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A. 7-2×(-![]() )=5×(-
)=5×(-![]() )=-1 B. -3÷7×
)=-1 B. -3÷7×![]() =-3÷1=-3
=-3÷1=-3
C. -32-(-3)2=-9-9=-18 D. 3×23-2×9=3×6-18=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
2 | 6 | 18 | 54 | 162…① |
-1 | 3 | 15 | 51 | 159…② |
-1 | -3 | -9 | -27 | -81…③ |
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数有什么关系?
(3)每行取第6个数计算它们的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式2a(b+c)-3(b+c)的结果是______.
【答案】(b+c)(2a-3)
【解析】解析:2a(b+c)-3(b+c)=(b+c)(2a-3).
点睛:因式分解的方法:(1)提取公因式法.ma+mb+mc=m(a+b+c).
(2)公式法:完全平方公式,平方差公式.
(3)十字相乘法.
因式分解的时候,要注意整体换元法的灵活应用,训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
17
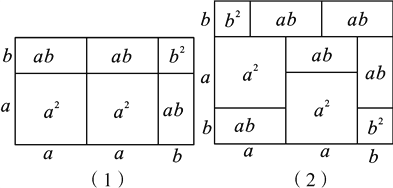
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com