
分析 原式分别利用小红与小明的解法计算即可.
解答 解:法1:原式的倒数为($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)÷(-$\frac{1}{42}$)=($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)×(-42)=-7+9-28+12=-35+21=-14,
∴(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)=-$\frac{1}{14}$;
法2:原式=(-$\frac{1}{42}$)÷[($\frac{1}{6}$+$\frac{2}{3}$)-($\frac{3}{14}$+$\frac{2}{7}$)]=-$\frac{1}{42}$÷($\frac{5}{6}$-$\frac{1}{2}$)=-$\frac{1}{42}$÷$\frac{1}{3}$=-$\frac{1}{42}$×3=-$\frac{1}{14}$.
点评 此题考查了有理数的混合运算,以及倒数,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
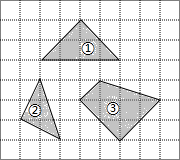 如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上,被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是②③.
如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上,被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是②③.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点B在⊙A内 | B. | 点C在⊙A上 | C. | y轴和⊙A相切 | D. | x轴和⊙A相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com