
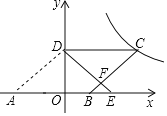
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限.将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=![]() (k≠0)图象经过点C,且S△BEF=
(k≠0)图象经过点C,且S△BEF=![]() ,则k的值为_____.
,则k的值为_____.
【答案】12
【解析】
连接OC,BD,由折叠的性质得OA=OE,由中点的性质得OA=2OB,设OB=BE=x,则OA=2x,通过证明△CDF∽△BEF,可得![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,再根据三角形面积的关系即可求出k的值.
,再根据三角形面积的关系即可求出k的值.
解:连接OC,BD,
∵将△AOD沿y轴翻折,使点A落在x轴上的点E处,
∴OA=OE,
∵点B恰好为OE的中点,
∴OE=2OB,
∴OA=2OB,
设OB=BE=x,则OA=2x,
∴AB=3x,
∵四边形ABCD是平行四边形,
∴CD=AB=3x,
∵CD∥AB,
∴△CDF∽△BEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∵S△BEF=![]() ,
,
∴S△BDF=![]() ,S△CDF=
,S△CDF=![]() ,
,
∴S△BCD=6,
∴S△CDO=S△BDC=6,
∴k=2S△CDO=12,
故答案为12.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 逆时针方向旋转,记旋转角为
逆时针方向旋转,记旋转角为![]() .
.
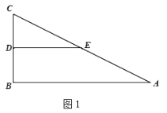

(1)问题发现
①当![]() 时,
时,![]() ____________;②当
____________;②当![]() 时,
时,![]() ___________.
___________.
(2)拓展探究试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() 三点在同一条直线上时,直接写出线段
三点在同一条直线上时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),两个等腰直角三角形ABC和DEF有一条边在同一条直线l上,DE=2,AB=1.将直线EB绕点E逆时针旋转45°,交直线AD于点M.将图(1)中的△ABC沿直线l向右平移,设C、E两点间的距离为k.请解答下列问题:
(1)①当点C与点F重合时,如图(2)所示,此时![]() 的值为 .
的值为 .
②在平移过程中,![]() 的值为 (用含k的代数式表示).
的值为 (用含k的代数式表示).
(2)将图(2)中的△ABC绕点C逆时针旋转,使点A落在线段DF上,如图(3)所示,将直线EB绕点E逆时针旋转45°,交直线AD于点M,请补全图形,并计算![]() 的值.
的值.
(3)将图(1)中的△ABC绕点C逆时针旋转α(0°<α≤45°),将直线EB绕点E逆时针旋转45°,交直线AD于点M,计算![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
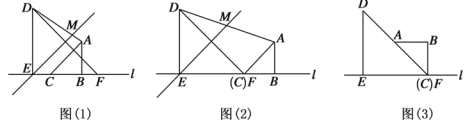
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.
(1)求出y与x的函数关系式;
(2)若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
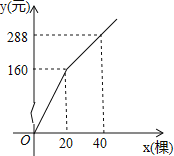
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=![]() (k>0)的图象上,则y1、y2、y3的大小关系是( )
(k>0)的图象上,则y1、y2、y3的大小关系是( )
A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
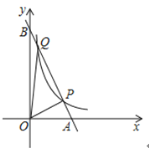
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com