
【题目】如图,在正△ABC中,D、E分别在AC、AB上,且 ![]() =
= ![]() , AE=BE , 则有( )
, AE=BE , 则有( ) 
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
【答案】D
【解析】解答:∵△ABC是等边三角形, ![]() =
= ![]() , ∴AB=BC=AC , ∠A=∠C ,
, ∴AB=BC=AC , ∠A=∠C ,
设AD=x , AC=3x ,
则BC=3x , CD=2x ,
∵AE=BE= ![]() x ,
x ,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴△AED∽△CBD;
故选:D .
分析:根据等边三角形的性质得出角相等,再由已知条件求出 ![]() =
= ![]()
, 即两边对应成比例并且夹角相等,因此两个三角形相似.
【考点精析】本题主要考查了相似三角形的判定的相关知识点,需要掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是 . (结果保留π) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路边有一根电线杆AB和一块正方形广告牌(不用考虑牌子的厚度).有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点,已知BC=5米,正方形边长为2米,DE=4米.则此时电线杆的高度是( )米.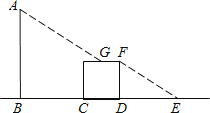
A.8
B.7
C.6
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD , AD=BC , 点E在边AD上,BE与AC相交于点O , 且∠ABE=∠BCA . 
(1)求证:△BAE∽△BOA.
(2)求证:BOBE=BCAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E , 则图中一定相似的三角形是( ) 
A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m. 
(1)若养鸡场面积为200m2 , 求鸡场靠墙的一边长.
(2)养鸡场面积能达到250m2吗?如果能,请给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为°. 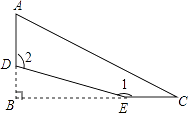
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.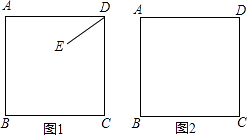
(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG= ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com