
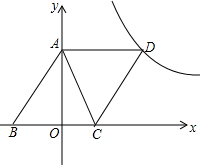
 如图,已知,A(0,4),B(-3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=$\frac{k}{x}$的图象经过D点.
如图,已知,A(0,4),B(-3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=$\frac{k}{x}$的图象经过D点.分析 (1)由A(0,4),B(-3,0),C(2,0),利用勾股定理可求得AB=5=BC,又由D为B点关于AC的对称点,可得AB=AD,BC=DC,即可证得AB=AD=CD=CB,继而证得四边形ABCD为菱形;
(2)由四边形ABCD为菱形,可求得点D的坐标,然后利用待定系数法,即可求得此反比例函数的解析式;
(3)由四边形ABMN是平行四边形,根据平移的性质,可求得点N的横坐标,代入反比例函数解析式,即可求得点N的坐标,继而求得M点的坐标.
解答 解:(1)∵A(0,4),B(-3,0),C(2,0),
∴OA=4,OB=3,OC=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,BC=5,
∴AB=BC,
∵D为B点关于AC的对称点,
∴AB=AD,CB=CD,
∴AB=AD=CD=CB,
∴四边形ABCD为菱形;
(2)∵四边形ABCD为菱形,
∴D点的坐标为(5,4),反比例函数y=$\frac{k}{x}$的图象经过D点,
∴4=$\frac{k}{5}$,
∴k=20,
∴反比例函数的解析式为:y=$\frac{20}{x}$;
(3)∵四边形ABMN是平行四边形,
∴AN∥BM,AN=BM,
∴AN是BM经过平移得到的,
∴首先BM向右平移了3个单位长度,
∴N点的横坐标为3,
代入y=$\frac{20}{x}$,
得y=$\frac{20}{3}$,
∴M点的纵坐标为:$\frac{20}{3}$-4=$\frac{8}{3}$,
∴M点的坐标为:(0,$\frac{8}{3}$).
点评 此题属于反比例函数综合题,考查了菱形的性质与判定、待定系数法求函数的解析式以及平行四边形的性质.注意掌握坐标与图形的关系是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | m | 93 | 93 | 12 |
| 九(2)班 | 99 | 95 | n | 93 | 8.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com