
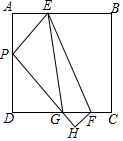
 现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.
现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.分析 (1)根据两角相等证明两三角形相似;
(2)三角形DPG的周长是一定值,不发生变化.由△AEP∽△DPG,两个三角形的周长的比是AE:PD,设AP=x,根据勾股定理可以用x表示出PD的长与△PAE的周长,根据周长的比等于相似比,即可求解.
解答 解:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠D=90°,
由折叠得:∠EPH=∠B=90°,
∴∠APE+∠DPG=∠APE+∠AEP=90°,
∴∠DPG=∠AEP,
∴△AEP∽△DPG;
(2)△PDG的周长保持不变,
设AP=x,则PD=4-x,
由折叠性质可知,EP=4-AE,
在Rt△AEP中,AE2+AP2=EP2,即AE2+x2=(4-AE)2,
整理得:AE2+x2=16-8AE+AE2,
∴AE=$\frac{16-{x}^{2}}{8}$,
由(1)得:△AEP∽△DPG,
∴△AEP的周长:△DPG的周长=AE:PD,
∴△DPG的周长=$\frac{△AEP的周长×PD}{AE}$=$\frac{(x+AE+4-AE)×(4-x)}{AE}$=(4+x)•(4-x)$÷\frac{16-{x}^{2}}{8}$=8,
∴△GDP的周长保持不变.
点评 此题考查了折叠的性质、正方形的性质、勾股定理以及相似三角形的判定与性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.| 关注情况 | 频数 | 频率 |
| A.高度关注 | k | 0.2 |
| B.一般关注 | m | 0.5 |
| C.极少关注 | 10 | n |
| D.不关注 | 5 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com