练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    以边长1的正方形的对角线为边长作第二个正方形，以第二个正方形的对角线为边长作第三个正方形，…，如此做下去得到第n个正方形．设第n个正方形的面积为Sn，通过运算找规律，可以猜想Sn=    ．
    【答案】分析：根据勾股定理和正方形的面积公式可分别求得第二个，第三个，第四个正方形的面积，从而找出规律求得Sn
    解答：解：根据勾股定理和正方形的面积公式得到：第二个正方形的面积是1+1=2，第三个正方形的面积是2+2=4=22，第四个正方形的面积是4+4=8=23，…依此类推，则Sn=2n-1
    点评：此题要能够结合勾股定理表示出正方形的面积．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：在Rt△ABC中，∠C=90°∠A、∠B、∠C所对的边分别记作a、b、c．
    （1）如图1，分别以△ABC的三条边为边长向外作正方形，其正方形的面积由小到大分别记作S1、S2、S3，则有S1+S2=S3；
    （2）如图2，分别以△ABC的三条边为直径向外作半圆，其半圆的面积由小到大分别记作S1、S2、S3，请问S1+S2与S3有怎样的数量关系，并证明你的结论；
    （3）分别以直角三角形的三条边为直径作半圆，如图3所示，其面积由小到大分别记作S1、S2、S3，根据（2）中的探索，直接回答S1+S2与S3有怎样的数量关系；
    （4）若Rt△ABC中，AC=6，BC=8，求出图4中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （附加题）工人师傅有两块板材边角料，其中一块是边长60cm的正方形板材；另一块是上底为30cm，下底为120cm，高为60cm的直角梯形板材（如下图①）．工人师傅想将这两块板材裁成两块全等的矩形板材，他将两块板材叠放在一起，使梯形的两个直角顶点分别与正方形的两个顶点重合，两块板材的重叠部分为五边形ABCFE围成的区域（如图②）．由于受材料纹理限制，要求裁出的矩形要以点B为一个顶点．
    （1）利用图②，求FC的长；
    （2）如图③，若矩形的一个顶点P在线段EF上，P点到BG的距离为PN，试证明：
    PN
    NG
    =
    2
    3
    ；
    （3）利用图③，求顶点B所对的顶点P到BC的距离PN为多少时，矩形PMBN的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    工人师傅有两块板材边角料，其中一块是边长60cm的正方形板材；另一块是上底为30cm，下底为120cm，高为60cm的直角梯形板材（如下图①）．工人师傅想将这两块板材裁成两块全等的矩形板材，他将两块板材叠放在一起，使梯形的两个直角顶点分别与正方形的两个顶点重合，两块板材的重叠部分为五边形ABCFE围成的区域（如图②）．由于受材料纹理限制，要求裁出的矩形要以点B为一个顶点．
    （1）利用图②，求FC的长；
    （2）如图③，若矩形的一个顶点P在线段EF上，P点到BG的距离为PN，试证明：数学公式；
    （3）利用图③，求顶点B所对的顶点P到BC的距离PN为多少时，矩形PMBN的面积最大？最大面积是多少？

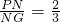    查看答案和解析>>

    科目：初中数学 来源： 题型：

    王师傅有两块板材边角料，其中一块是边长为60 cm的正方形板子；另一块是上底为30 cm，下底为120 cm，高为60 cm的直角梯形板子(如图①)，王师傅想将这两块板子裁成两块全等的矩形板材。他将两块板子叠放在一起，使梯形的两个直角顶点分别与正方形的两个顶点重合，两块板子的重叠部分为五边形ABCFE围成的区域(如图②)，由于受材料纹理的限制，要求裁出的矩形要以点B为一个顶点。

    (1)求FC的长；

    (2)利用图②求出矩形顶点B所对的顶点到BC边的距离(cm)为多少时，矩形的面积最大?最大面积时多少?

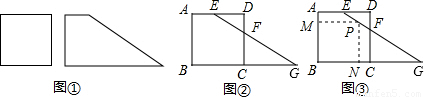
    (3)若想使裁出的矩形为正方形，试求出面积最大的正方形的边长．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年深圳市福田区翰林学校九年级（上）期中数学试卷（解析版） 题型：解答题

    （附加题）工人师傅有两块板材边角料，其中一块是边长60cm的正方形板材；另一块是上底为30cm，下底为120cm，高为60cm的直角梯形板材（如下图①）．工人师傅想将这两块板材裁成两块全等的矩形板材，他将两块板材叠放在一起，使梯形的两个直角顶点分别与正方形的两个顶点重合，两块板材的重叠部分为五边形ABCFE围成的区域（如图②）．由于受材料纹理限制，要求裁出的矩形要以点B为一个顶点．
    （1）利用图②，求FC的长；
    （2）如图③，若矩形的一个顶点P在线段EF上，P点到BG的距离为PN，试证明：；
    （3）利用图③，求顶点B所对的顶点P到BC的距离PN为多少时，矩形PMBN的面积最大？最大面积是多少？

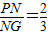    查看答案和解析>>

    同步练习册答案