
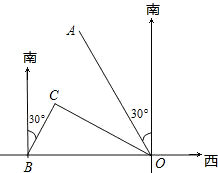
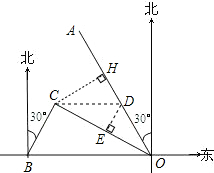
 近期由于南海争端频发,我国的渔船经常受到一些干扰,有关部门决定派遣渔政执法船护渔.如图,港口B位于港口O正东方向120km处,小岛C位于港口O南偏东60°的方向.一队渔船从港口O出发,以20km/h的速度沿南偏东30°的OA方向驶离港口O.同时一艘渔政执法船从港口B出发,以60km/h的速度沿南偏西30°的方向驶向小岛C,并要在小岛C上停留1小时补给物资,然后按原来的速度向渔船编队驶去.
近期由于南海争端频发,我国的渔船经常受到一些干扰,有关部门决定派遣渔政执法船护渔.如图,港口B位于港口O正东方向120km处,小岛C位于港口O南偏东60°的方向.一队渔船从港口O出发,以20km/h的速度沿南偏东30°的OA方向驶离港口O.同时一艘渔政执法船从港口B出发,以60km/h的速度沿南偏西30°的方向驶向小岛C,并要在小岛C上停留1小时补给物资,然后按原来的速度向渔船编队驶去. ,
,

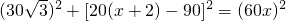 ,
, (舍去)
(舍去)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 近期由于南海争端频发,我国的渔船经常受到一些干扰,有关部门决定派遣渔政执法船护渔.如图,港口B位于港口O正东方向120km处,小岛C位于港口O南偏东60°的方向.一队渔船从港口O出发,以20km/h的速度沿南偏东30°的OA方向驶离港口O.同时一艘渔政执法船从港口B出发,以60km/h的速度沿南偏西30°的方向驶向小岛C,并要在小岛C上停留1小时补给物资,然后按原来的速度向渔船编队驶去.
近期由于南海争端频发,我国的渔船经常受到一些干扰,有关部门决定派遣渔政执法船护渔.如图,港口B位于港口O正东方向120km处,小岛C位于港口O南偏东60°的方向.一队渔船从港口O出发,以20km/h的速度沿南偏东30°的OA方向驶离港口O.同时一艘渔政执法船从港口B出发,以60km/h的速度沿南偏西30°的方向驶向小岛C,并要在小岛C上停留1小时补给物资,然后按原来的速度向渔船编队驶去.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com