练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
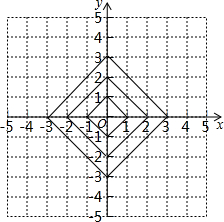
    5．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，如图，由里向外数的第2各正方形开始，分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1，2，3，…得到的，请你观察图形，猜想由里向外第12个正方形四条边上的整点个数为48．

    分析 根据第一个正方形可以得到整点个数为4，第二个正方形可知除顶点外每条边上的整点个数为1，故第二个正方形四条边上的整点个数为：4×1+4，同理可知，第三个正方形四条边上的整点个数为：4×2+4，从而可以得到第12个正方形四条边上的整点个数为．

    解答 解：根据题意可得，第一个正方形四条边上的整点个数为：4；
    第二个正方形四条边上的整点个数为：4×1+4=8；
    第三个正方形四条边上的整点个数为：4×2+4=12；
    由此可得，由里向外第12个正方形四条边上的整点个数为：4×11+4=48．
    故答案为：48．

    点评 本题考查规律性：点的坐标，解题的关键是观察各个正方形，能发现正方形四条边上的整点数的规律．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．如图：两个同心圆，其中大圆的弦AD交小圆于C、D两点那么：AB与CD相等吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

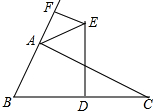    19．如图，已知△ABC，DE垂直平分BC边，∠BAC外角平分线与DE交于E，过E作EF垂直直线AB于F．若AF=3，AB=7，那么AC长是13．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，直线l交线段AB于点P，AC⊥l，BD⊥l，垂足分别为C、D，M是AB的中点，求证：MC=MD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

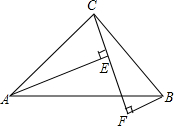    20．如图，已知：∠BAC=∠ABC，CE=BF，AE⊥CF，BF⊥CF，C、E、F分别为垂足
    （1）求证：△BCF≌△CAE；
    （2）根据第（1）题的结论判断线段AE、BF、EF的大小关系．并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若a是有理数，则下列判断正确的是（　　）
    A．|a|是正数B．-a是负数C．|a|是正数或0D．|-a|是负数或0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．某种商品的进价为每件50元，售价为每件60元，每个月可卖出200件；如果每件上平的售价上涨1元，则每个月少卖10件，那么这个月的最大利润2250元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，⊙O1与⊙O2交于A、B两点，P是⊙O1上的点，连接PA、PB交⊙O2于C、D，求证：PO1⊥CD．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷（解析版） 题型：单选题

    设n为正整数，且n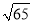＜＜n+1，则n的值为（ ）

    A. 5 B. 6 C. 7 D. 8

    查看答案和解析>>

    同步练习册答案