
【题目】如图, ABCD 为正方形, O 为 AC 、 BD 的交点,在![]() 中,
中,![]() 90,
90, ![]() 30,若OE
30,若OE ![]() ,则正方形的面积为( )
,则正方形的面积为( )
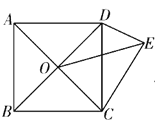
A. 5B. 4C. 3D. 2
【答案】B
【解析】
过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,判断出四边形OMEN是矩形,根据矩形的性质可得∠MON=90°,再求出∠COM=∠DON,根据正方形的性质可得OC=OD,然后利用“角角边”证明△COM和△DON全等,根据全等三角形对应边相等可得OM=ON,然后判断出四边形OMEN是正方形,设正方形ABCD的边长为![]() ,根据直角三角形30°角所对的直角边等于斜边的一半可得DE=
,根据直角三角形30°角所对的直角边等于斜边的一半可得DE=![]() CD,再利用勾股定理列式求出CE,根据正方形的性质求出OC=OD=
CD,再利用勾股定理列式求出CE,根据正方形的性质求出OC=OD=![]() a,然后利用四边形OCED的面积列出方程求出
a,然后利用四边形OCED的面积列出方程求出![]() ,再根据正方形的面积公式列式计算即可得解.
,再根据正方形的面积公式列式计算即可得解.
解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
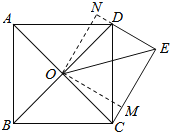
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
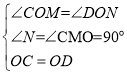 ,
,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
设正方形ABCD的边长为![]() ,则OC=OD=
,则OC=OD=![]()
∵∠CED=90°,∠DCE=30°,
∴DE=![]() CD=
CD=![]() ,
,
由勾股定理得,CE=![]() ,
,
∴四边形OCED的面积=![]() ,
,
解得![]() ,
,
所以,正方形ABCD的面积=![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】)6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下统计图:
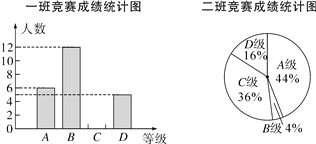
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答问题:
阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放八....按这个方法放满整个棋盘就行.”国王以为要不了多少粮食,就随口答应了.
(1)国际象棋的棋盘共有![]() 个格子,则在第
个格子,则在第![]() 格中应放 粒米.(用幂表示)
格中应放 粒米.(用幂表示)
(2)请探究第(1)题中的幂的个位数字是多少?(简要写出探究过程)
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
“用分数表示无限循环小数:![]()
解:设![]() .等式两边同时乘
.等式两边同时乘![]() ,
,
得![]() .
.
将![]() 得:
得:![]() ,
,
则![]()
![]()
请参照以上解法求出国王输给阿基米德的米粒数.(用幂的形式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,
,![]() .
.
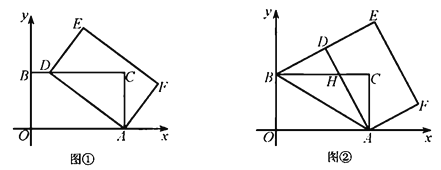
(Ⅰ)如图①,当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 的坐标;
的坐标;
(Ⅱ)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 交于点
交于点![]() .
.
①求证![]() ;
;
②求点![]() 的坐标.
的坐标.
(Ⅲ)记![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 的面积,求
的面积,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,OC是BO的延长线,OF平分∠AOD,∠AOE=35.
,OC是BO的延长线,OF平分∠AOD,∠AOE=35.
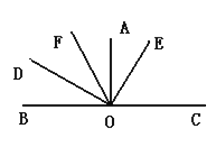
(1)求∠EOC的度数;
(2)求∠BOF的度数;
(3)请你写出图中三对相等的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )
①![]() 是
是![]() 次多项式,
次多项式,![]() 是
是![]() 次多项式(
次多项式(![]() 和
和![]() 都是正整数),则
都是正整数),则![]() 和
和![]() 一定都是
一定都是![]() 次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③
次多项式;②分式方程无解,则分式方程去分母后所得的整式方程无解;③![]() 为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变
为正整数);④分式的分子和分母都乘以(或除以)同一个整数,分式的值不变
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市某商场通过互联网销售某品牌新型台灯,第一周的总销售额为4000元,第二周的总销售额为4520元,第二周比第一周多售出13盏台灯.
(1)求每盏台灯的售价;
(2)该公司在第三周将每盏台灯的售价降低了![]() ,并预计第三周能售出140盏灯恰逢期末考试,极大的提高了中学生使用台灯的数量,该款台灯在第三周的销量比预计的140盏还多了
,并预计第三周能售出140盏灯恰逢期末考试,极大的提高了中学生使用台灯的数量,该款台灯在第三周的销量比预计的140盏还多了![]() .已知每盏台灯的成本为16元,该公司第三周销售台灯的总利润为5040元,求
.已知每盏台灯的成本为16元,该公司第三周销售台灯的总利润为5040元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com