

分析 (1)根据A类的人数和所占的百分比求出总人数,再乘以B所占的百分比求出喜欢B的人数,用喜欢C、D的人数除以总人数即可求出C、D所占的百分比,从而补全统计图;
(2)用全校的总人数乘以喜欢“阮经天”的人数所占的百分比,即可得出答案.
解答 解:(1)本次被调查的学生有$\frac{40}{20%}$=200(人);
B的人数是;200×25%=50(人),
C所占的百分比是:$\frac{20}{200}$×100%=10%;
D所占的百分比是:$\frac{60}{200}$×100%=30%;
补图如下: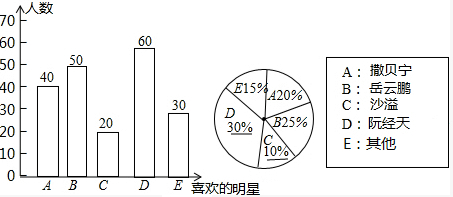
故答案为:200;
(2)根据题意得:
3500×30%=1050(人),
答:估计全校喜欢“阮经天”的人数有1050人.
点评 此题考查了条形统计图和扇形统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了用样本估计总体的思想.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为α,已知sinα=$\frac{3}{5}$,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.
数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为α,已知sinα=$\frac{3}{5}$,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.| A. | 7.4 | B. | 7.2 | C. | 7 | D. | 6.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com