
【题目】如图,在![]() 中,AD是BC边上的高,
中,AD是BC边上的高,![]() 。
。

(1)求证:AC=BD
(2)若![]() ,求AD的长。
,求AD的长。
【答案】(1)证明见解析;(2)8
【解析】
(1)由于tanB=cos∠DAC,所以根据正切和余弦的概念证明AC=BD;
(2)设AD=12k,AC=13k,然后利用题目已知条件即可解直角三角形.
(1)证明:∵AD是BC上的高,
∴AD⊥BC,
∴∠ADB=90°,∠ADC=90°,
在Rt△ABD和Rt△ADC中,
∵tanB=![]() ,cos∠DAC=
,cos∠DAC=![]() ,
,
又∵tanB=cos∠DAC,
∴![]() =
=![]() ,
,
∴AC=BD;
(2)在Rt△ADC中,sinC=![]() ,
,
故可设AD=12k,AC=13k,
∴CD=![]() =5k,
=5k,
∵BC=BD+CD,又AC=BD,
∴BC=13k+5k=18k,
由已知BC=12,
∴18k=12,
∴k=![]() ,
,
∴AD=12k=12×![]() =8.
=8.


科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,盘锦市某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.

根据图中信息解决下列问题:
(1)本次共调查______名学生,扇形统计图中B所对应的扇形的圆心角为______度;
(2)补全条形统计图;
(3)该校参加实践活动课的学生共1200人,求该校参加D类实践活动课的学生大约多少人?
(4)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在![]() 上,过点C作
上,过点C作![]() 交OB延长线于点A,连接CD,且
交OB延长线于点A,连接CD,且![]() ,
,![]() .
.
(1)直线AC与![]() 有怎样的位置关系?为什么?
有怎样的位置关系?为什么?
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是
是![]() 的内接正方形,
的内接正方形,![]() ,
,![]() 、
、![]() 是
是![]() 的两 条切线,
的两 条切线,![]() 、
、![]() 为切点.
为切点.
(1)如图1,求![]() 的半径;
的半径;
(2)如图1,若点![]() 是
是![]() 的中点,连结
的中点,连结![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,若点![]() 是
是![]() 边上任意一点(不含
边上任意一点(不含![]() 、
、![]() ),以点
),以点![]() 为直角顶点,在
为直角顶点,在![]() 的上方作
的上方作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)在平面直角坐标系中画出与△ABC关于点P(1,0)成中心对称的△A'B'C',并分别写出点A',B',C'的坐标;
(2)如果点M(a,b)是△ABC边上(不与A,B,C重合)任意一点,请写出在△A'B'C'上与点M对应的点M'的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
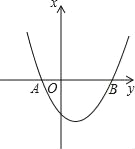
【题目】抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式.
(2)一动点P在(1)中抛物线上滑动且满足S△ABP=10,求此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧),
中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧),![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.

(1)当OB=2时,求点D的坐标.
(2)若点![]() 和点
和点![]() 在同一个反比例函数图象上,求
在同一个反比例函数图象上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
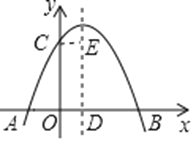
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E.现有下列结论:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正确结论的序号是 _____________________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com