
分析 (1)由1名男生和3名女生中随机抽取参加“我爱苏州”演讲比赛,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好是2名女生的情况,再利用概率公式即可求得答案.
解答 解:(1)∵1名男生和3名女生中随机抽取参加“我爱苏州”演讲比赛,
∴抽取1名,恰好是男生的概率为:$\frac{1}{4}$;
故答案为:$\frac{1}{4}$;
(2)画树状图得: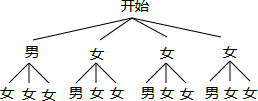
∵共有12种等可能的结果,恰好是2名女生的有6种情况,
∴恰好是2名女生的概率为:$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
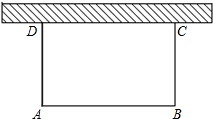 如图,用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD,已知墙长14m,设边AD的长为x(m),矩形ABCD的面积为y(m2).
如图,用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD,已知墙长14m,设边AD的长为x(m),矩形ABCD的面积为y(m2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
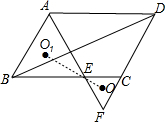 如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心
如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com