
【题目】如图, ![]() 是直线
是直线![]() 上的两点,直线l1、l2的初始位置与直线
上的两点,直线l1、l2的初始位置与直线![]() 重合将l1绕点
重合将l1绕点![]() 顺时针以每秒10°的速度旋转,将l2绕点B逆时针以每秒5°的速度旋转,且两条直线从重合位置同时开始旋转,设旋转时间为
顺时针以每秒10°的速度旋转,将l2绕点B逆时针以每秒5°的速度旋转,且两条直线从重合位置同时开始旋转,设旋转时间为![]() 秒(
秒(![]() 是正整数).当
是正整数).当![]() 时,设
时,设![]() 的交点为
的交点为![]() ;当
;当![]() 时,设
时,设![]() 的交点为
的交点为![]() ;当
;当![]() 时设
时设![]() 的交点为
的交点为![]() ……那么当
……那么当![]() 时,
时, ![]() 相交所得的钝角是__________.当
相交所得的钝角是__________.当![]() 落在
落在![]() 上方时,
上方时, ![]() 的最小值是__________.
的最小值是__________.

科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:
(约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:![]() ).
).
第一步:在矩形纸片一端 ,利用图1的方法折出一个正方形,然后把纸片展平;
第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平;
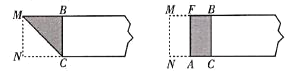
图1 图2
第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处;
处;
第四步:展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ,则图4中就会出现黄金矩形.
,则图4中就会出现黄金矩形.
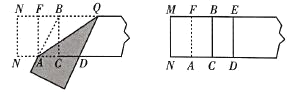
图3 图4
(1)在图3中![]() _________ (保留根号);
_________ (保留根号);
(2)如图3,则四边形![]() 的形状是_________;
的形状是_________;
(3)在图4中黄金矩形是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
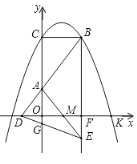
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
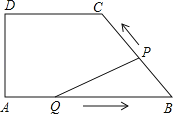
(1)当t为何值时,P,Q两点同时停止运动;
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
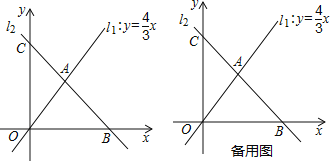
【题目】如图,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() .
.
(1)求直线![]() 的关系式;
的关系式;
(2)若与![]() 轴平行的直线
轴平行的直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、点
、点![]() ,则
,则![]() 的面积为_____(直接填空);
的面积为_____(直接填空);
(3)在(2)的情况下,把![]() 沿着过原点的直线
沿着过原点的直线![]() 翻折,当点
翻折,当点![]() 落在直线
落在直线![]() 上时,直接写出
上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月15日,我国“两会”落下帷幕.13天时间里,来自各地的5000余名代表、委员聚于国家政治中心,共议国家发展大计.某校初三(3)班张老师为了了解同学们对“两会”知识的知晓情况,进行了一次小测试,测试满分100分.其中
A组同学的测试成绩分别为:91 91 86 93 85 89 89 88 87 91
B组同学的测试成绩分别为:88 97 88 85 86 94 84 83 98 87
根据以上数据,回答下列问题:
(1)完成下表:
组别 | 平均数 | 中位数 | 众数 | 方差 |
A组 | 89 | 89 | b | c |
B组 | 89 | a | 88 | 26.2 |
其中a= ,b= ,c= ,
(2)张老师将B组同学的测试成绩分成四组并绘制成如图所示频数分布直方图(不完整),请补全;
(3)根据以上分析,你认为 组(填“A”或“B”)的同学对今年“两会”知识的知晓情况更好一些,请写出你这样判断的理由(至少写两条):① ② .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动速度都是
同时出发,运动速度都是![]() ,点
,点![]() 由
由![]() 向
向![]() 运动;点
运动;点![]() 由
由![]() 向
向![]() 运动,当
运动,当![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点运动停止,设时间为
两点运动停止,设时间为![]() 秒
秒![]() .连接
.连接![]() ,
,![]() ,
,![]() .
.
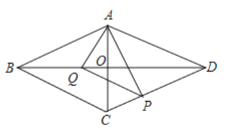
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)设![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是四边形
的面积是四边形![]() 面积的
面积的![]() ;
;
(4)是否存在![]() 值,使得线段
值,使得线段![]() 经过
经过![]() 的中点
的中点![]() ;若存在,求出
;若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
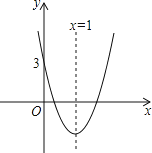
A. ②③④B. ①②③C. ②③D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com