
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD 和折线 OABC 表示“龟兔赛跑”时的路程与时间关系,请你根据图中给出的信息,解决下列问题:
(1)折线 OABC 表示赛跑过程中_______的路程与时间的关系, 线段 OD 表示赛跑过程中_______的路程与时间的关系, 赛跑的全程是________米.
(2)兔子在起初每分钟跑多少米,乌龟用多少分钟追上了正在睡觉的兔子.
(3)兔子醒来,以 48 千米/小时的速度跑向终点,结果还是比乌龟晚到 0.5 分钟,请你算算兔子中间停下睡觉用了多少分钟?

【答案】(1)兔子,乌龟,1500;(2)兔子在起初每分钟跑700米,乌龟用14分钟追上了正在睡觉的兔子;(3)兔子中间停下睡觉用了28.5分钟.
【解析】
(1)利用乌龟始终运动,中间没有停留,进而得出折线 OABC和线段OD的意义和全程的距离;
(2)根据乌龟的速度及兔子睡觉时的路程即可得;
(3)用乌龟跑完全程的时间+兔子晚到的时间兔子在路上奔跑的两端所用时间可得.
解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻;
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
线段 OD 表示赛跑过程中乌龟的路程与时间的关系
由图象可知:赛跑的路程为1500米;
故答案为:兔子,乌龟,1500;
(2)结合图象得出:兔子在起初每分钟跑700米.
1500÷30=50(米)
∴乌龟每分钟爬50米.
700÷50=14(分钟)
∴乌龟用14分钟追上了正在睡觉的兔子.
(3)48 千米/小时=800米/分,
30+0.51(1500700)÷800=28.5(分钟),
∴兔子中间停下睡觉用了28.5分钟.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
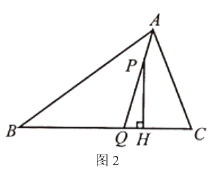
【题目】在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 重合),
重合),![]() 于点
于点![]() .
.
(1)若![]() ,如图1,当点
,如图1,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的度数;
的度数;

(2)当![]() 是锐角三角形时,如图2,试探索
是锐角三角形时,如图2,试探索![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 不在同一条直线上,
不在同一条直线上,![]()
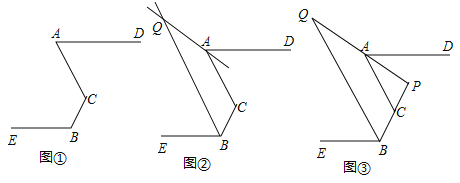
(1)如图①,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,![]() 分别为
分别为![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图③,在(2)的前提下且![]() ,
,![]() ,直接写
,直接写![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3y)(4x﹣3x2﹣1);
(2)(2x+3)(x﹣7);
(3)(-1)2019+(3-π)0 +2-2+ 4101×0.25100;
(4)2019220182020.(运用乘法公式计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行线问题的探索:
(1)问题一:已知:如图,![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数
的度数
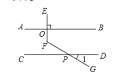
甲、乙.丙三位同学用不同的方法添加辅助线解决问题,如图1:
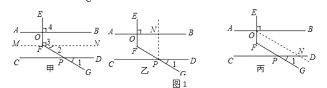
甲同学辅助线的做法和分析思路如下:辅助线:过点![]() 作
作![]() ,分析思路:
,分析思路:
a.欲求![]() 的度数,由图可知只需转化为求
的度数,由图可知只需转化为求![]() 和
和![]() 的度数;
的度数;
b.![]() 可知,
可知,![]() 又由已知
又由已知![]() 的度数可得
的度数可得![]() 的度数;
的度数;
c.由![]() 推出
推出![]() 由此可推出
由此可推出![]() ;
;
d.由已知![]() 可得
可得![]() 所以可得
所以可得![]() 的度数;
的度数;
f.从而可求![]() 的度数
的度数
①请你根据乙同学所画的图形,描述乙同学辅助线的做法.辅助线: _;
②请你根据丙同学所画的图形,且不再添加其他辅助线,求![]() 的度数.
的度数.
(2)问题二: 如图2,在平面直角坐标系中,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 其中
其中![]() 满足关系式:
满足关系式:![]() .
.
①![]() ,
,![]() ;
;
②根据已知点的坐标判断![]() 与
与![]() 的位置关系是
的位置关系是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c满足:a+c<0,ac>0,|b|=b,
(1)比较大小:a______0;b_____;c_____0;
(2)先去绝对值,再化简:|a﹣2b+c|﹣![]() +2|b﹣2c|的值.
+2|b﹣2c|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
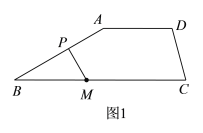
【题目】已知:AD∥BC,点P为直线AB上一动点,点M在线段BC上,连接MP,![]() ,
,![]() ,
,![]() .
.
(1)如图1,当点P在线段AB上时,若![]() ,
,![]() =150°,则
=150°,则![]() =________°;
=________°;
(2)如图2,当点P在AB的延长线上时,写出![]() ,
,![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;

(3)如图3,当点P在BA的延长线上时,请画出图形,直接写出![]() ,
,![]() 与
与![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com