
分析 (1)原式利用单项式乘以单项式法则计算即可得到结果;
(2)原式逆用积的乘方运算法则计算即可得到结果;
(3)原式利用零指数幂、负整数指数幂法则计算即可得到结果;
(4)原式利用完全平方公式化简,合并即可得到结果;
(5)原式变形后,利用同分母分式的除法法则计算即可得到结果.
解答 解:(1)原式=20×109=2×1010;
(2)原式=(0.125×2×4)6=1;
(3)原式=1+9=10;
(4)原式=a2-2ab+b2+a2+2ab+b2=2a2+2b2;
(5)原式=(q-q)4÷(q-p)3=q-p.
故答案为:(1)2×1010;(2)1;(3)10;(4)2a2+2b2;(5)q-p
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:填空题
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
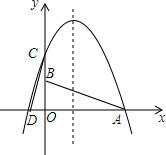 如图,已知,A点坐标是(3,0),B点坐标是(0,1),将△AOB绕点O逆时针旋转90°得到△COD,A、B旋转后的对应点分别为C和D,抛物线y=-x2+bx+c经过C、D两点.
如图,已知,A点坐标是(3,0),B点坐标是(0,1),将△AOB绕点O逆时针旋转90°得到△COD,A、B旋转后的对应点分别为C和D,抛物线y=-x2+bx+c经过C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
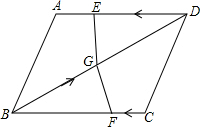 如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题:
如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com