练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．将正整数按如图所示的规律排列，若有序实数对（n，m）表示第n排从左到右第m个数，如（4，3）表示整数9，则（10，8）表示的整数为（　　）
    A．98B．53C．54D．52

    分析 根据排列规律解答，从图中可以发观，第n排的最后的数为：$\frac{1}{2}$n（n+1）．

    解答 解：从图中可以发观，第n排的最后的数为：$\frac{1}{2}$n（n+1）
    ∵第9排最后的数为：$\frac{1}{2}$×9×（9+1）=45，
    ∴（10，8）表示第10排第8个数，则第10排第8个数为45+8=53．
    故选：B．

    点评 本题主要考查了学生阅读理解及总结规律的能力，找到第n排的最后的数的表达式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图，抛物线y=$\frac{1}{2}$x2+bx+c与y轴交于点C（0，-4），与x轴交于点A、B，且B点的坐标为（2，0）．
    （1）求抛物线的解析式；
    （2）若点P是AB上的一个动点，过点P作PE∥AC交BC于点E，连接CP，求△PCE面积的最大值；
    （3）在（2）的条件下，若点D为OA的中点，点M是线段AC上一点，当△OMD为等腰三角形时，连接MP、ME，把△MPE沿着PE翻折，点M的对应点为点N，求点N的坐标，并判断点N是否在抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，已知梯形ABCD的四个顶点坐标分别为A（-2，1），B（-3，-2），C（3，-2），D（1，1），求梯形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}{x-2y=k}\\{2x+3y=k+1}\end{array}\right.$的解的和等于1，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

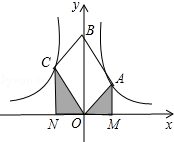    19．如图，OABC是平行四边形，对角线OB在y轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线$y=\frac{k_1}{x}$和y=$\frac{{k}_{2}}{x}$的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：①$\frac{AM}{CN}$=$\frac{|{k}_{1}|}{|{k}_{2}|}$；②阴影部分面积是$\frac{1}{2}$（k1+k2）；③当∠AOC=90°时，|k1|=|k2|；④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．其中正确的结论是（　　）
    A．①②③B．②④C．①③④D．①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解方程组：
    （1）$\left\{\begin{array}{l}{a：b：c=3：4：5}\\{a+b+c=36}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}-z=-5}\\{\frac{x}{3}-\frac{y}{2}+\frac{z}{2}=10}\\{\frac{x}{2}-\frac{y}{3}-\frac{z}{4}=6}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，△ABC中，∠C=90°，AD是角平分线，DE⊥AB于点E，CD=3，BC=8，则BE=（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知函数y=2x+1的图象经过P1（x1，y1），P2（x2，y2），如果y1＞y2，则x1x1＞x2x2（填“＞”，“＜”或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知直线y=2x，将其向下平移4个单位，所得直线的函数解析式为y=2x-4．

    查看答案和解析>>

    同步练习册答案