练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    有这样一道计算题：
    计算（２x3－３x2y－２xy2）－（x3－2xy2＋y3）＋（－x3＋３x2y－y3）的值，其中x=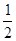，y=－1。甲同学把x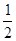＝错看成x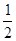＝－，但计算结果仍正确，你说是怎么一回事？

    解：（２x3－３x2y－２xy2）－（x3－2xy2＋y3）＋（－x3＋３x2y－y3）
    =２x3－３x2y－２xy2－x3＋2xy2－y3－x3＋３x2y－y3
    =－2 y3
    此式中没有含x字母的项，当y=－1时，原式=2与x无关。

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

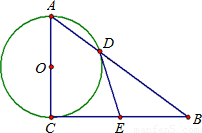
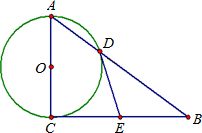    几何课本第三册复习题七中有这样一道几何题：以Rt△ABC的直角边AC为直径作圆，精英家教网交斜边AB于点D，过点D作圆的切线．求证：这条切线平分另一条直角边BC．（不必证明）
    现将上述习题改变成如下问题，请你解答：
    如图，以Rt△ABC的直角边AC为直径作⊙O，交斜边AB于点D，E为BC边的中点，连DE．
    （1）判断DE是否为⊙O的切线，并证明你的结论．
    （2）当AD：DB=9：16时，DE=8cm时，求⊙O的半径R．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题，就是“引葭赴岸”问题，题目是：
    “今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适马岸齐，问水深，葭长各几何？”
    题意是：有一正方形池塘，边长为一丈，有棵芦苇长在它的正中央，高出水面部分有一尺长，把芦苇拉向岸边，恰好碰到岸沿，问水深和芦苇长各是多少？

    查看答案和解析>>

    科目：初中数学 来源：第3章《直线与圆、圆与圆的位置关系》中考题集（23）：3.1 直线与圆的位置关系（解析版） 题型：解答题

    几何课本第三册复习题七中有这样一道几何题：以Rt△ABC的直角边AC为直径作圆，交斜边AB于点D，过点D作圆的切线．求证：这条切线平分另一条直角边BC．（不必证明）
    现将上述习题改变成如下问题，请你解答：
    如图，以Rt△ABC的直角边AC为直径作⊙O，交斜边AB于点D，E为BC边的中点，连DE．
    （1）判断DE是否为⊙O的切线，并证明你的结论．
    （2）当AD：DB=9：16时，DE=8cm时，求⊙O的半径R．

    查看答案和解析>>

    科目：初中数学 来源：第5章《中心对称图形（二）》中考题集（44）：5.5 直线与圆的位置关系（解析版） 题型：解答题

    几何课本第三册复习题七中有这样一道几何题：以Rt△ABC的直角边AC为直径作圆，交斜边AB于点D，过点D作圆的切线．求证：这条切线平分另一条直角边BC．（不必证明）
    现将上述习题改变成如下问题，请你解答：
    如图，以Rt△ABC的直角边AC为直径作⊙O，交斜边AB于点D，E为BC边的中点，连DE．
    （1）判断DE是否为⊙O的切线，并证明你的结论．
    （2）当AD：DB=9：16时，DE=8cm时，求⊙O的半径R．

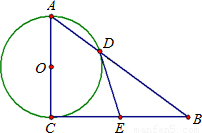
    查看答案和解析>>

    科目：初中数学 来源：第24章《圆》中考题集（44）：24.2 点、直线和圆的位置关系（解析版） 题型：解答题

    几何课本第三册复习题七中有这样一道几何题：以Rt△ABC的直角边AC为直径作圆，交斜边AB于点D，过点D作圆的切线．求证：这条切线平分另一条直角边BC．（不必证明）
    现将上述习题改变成如下问题，请你解答：
    如图，以Rt△ABC的直角边AC为直径作⊙O，交斜边AB于点D，E为BC边的中点，连DE．
    （1）判断DE是否为⊙O的切线，并证明你的结论．
    （2）当AD：DB=9：16时，DE=8cm时，求⊙O的半径R．

    查看答案和解析>>

    同步练习册答案