
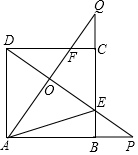
 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=$\frac{13}{16}$,其中正确结论的个数是( )
如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=$\frac{13}{16}$,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由四边形ABCD是正方形,得到AD=BC,∠DAB=∠ABC=90°,根据全等三角形的性质得到∠P=∠Q,根据余角的性质得到AQ⊥DP;故①正确;根据相似三角形的性质得到AO2=OD•OP,由OD≠OE,得到OA2≠OE•OP;故②错误;根据全等三角形的性质得到CF=BE,DF=CE,于是得到S△ADF-S△DFO=S△DCE-S△DOF,即S△AOD=S四边形OECF;故③正确;根据相似三角形的性质得到BE=$\frac{3}{4}$,求得QE=$\frac{13}{4}$,QO=$\frac{13}{5}$,OE=$\frac{39}{20}$,由三角函数的定义即可得到结论.
解答 解:∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,$\left\{\begin{array}{l}{AD=AB}\\{∠DAP=∠ABQ}\\{AP=BQ}\end{array}\right.$,
∴△DAP≌△ABQ,
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP;
故①正确;
∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴$\frac{AO}{OD}=\frac{OP}{OA}$,
∴AO2=OD•OP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OE•OP;故②错误;
在△CQF与△BPE中$\left\{\begin{array}{l}{∠FCQ=∠EBP}\\{∠Q=∠P}\\{CQ=BP}\end{array}\right.$,
∴△CQF≌△BPE,
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,$\left\{\begin{array}{l}{AD=CD}\\{∠ADC=∠DCE}\\{DF=CE}\end{array}\right.$,
∴△ADF≌△DCE,
∴S△ADF-S△DFO=S△DCE-S△DOF,
即S△AOD=S四边形OECF;故③正确;
∵BP=1,AB=3,
∴AP=4,
∵△PBE∽△DAP,
∴$\frac{PB}{EB}=\frac{PA}{DA}=\frac{4}{3}$,
∴BE=$\frac{3}{4}$,∴QE=$\frac{13}{4}$,
∵△QOE∽△PAD,
∴$\frac{QO}{PA}=\frac{OE}{AD}=\frac{QE}{PD}=\frac{\frac{13}{4}}{5}$,
∴QO=$\frac{13}{5}$,OE=$\frac{39}{20}$,
∴AO=5-QO=$\frac{12}{5}$,
∴tan∠OAE=$\frac{OE}{OA}$=$\frac{13}{16}$,故④正确,
故选C.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,三角函数的定义,熟练掌握全等三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:填空题
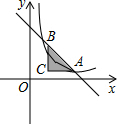 如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上,若双曲线y=$\frac{k}{x}$(x>0)与△ABC总有公共点,则k的取值范围是2≤k≤9.
如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上,若双曲线y=$\frac{k}{x}$(x>0)与△ABC总有公共点,则k的取值范围是2≤k≤9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩/分 | 66 | 67 | 68 | 69 | 70 |
| 人数 | 1 | 4 | 1 | 2 | 2 |
| A. | 67,67.5 | B. | 68,68 | C. | 68,67.5 | D. | 67.5,68 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
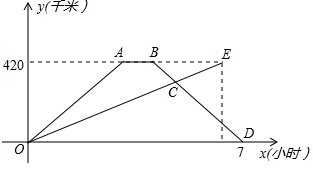 快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与所用的时间x(时)的关系如图所示,下列说法错误的是( )
快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与所用的时间x(时)的关系如图所示,下列说法错误的是( )| A. | 快车返回的速度为140千米/时 | |
| B. | 慢车的速度为70千米/时 | |
| C. | 快慢两车出发4$\frac{1}{2}$小时时两车相遇 | |
| D. | 出发$\frac{14}{3}$小时时,快慢两车距各自出发地的路程相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
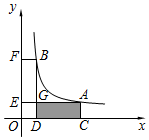 如图,A(a,b),B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A,B分别作x轴、y轴的垂线,垂足分别为C,D,E,F,AE,BD交于点G.则四边形ACDG的面积随着a的增大( )
如图,A(a,b),B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A,B分别作x轴、y轴的垂线,垂足分别为C,D,E,F,AE,BD交于点G.则四边形ACDG的面积随着a的增大( )| A. | 而增大 | B. | 而减小 | ||
| C. | 保持不变 | D. | 成反比例关系减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
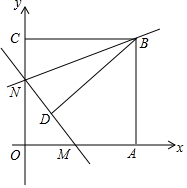 如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+$\sqrt{y-13}$=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=$\frac{3}{4}$
如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x-15|+$\sqrt{y-13}$=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=$\frac{3}{4}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
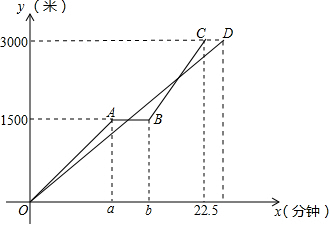 “低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com