
【题目】如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.

将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
五边形数 | 1 | 5 | 12 | 22 | c | 51 | 70 | … |
(1)按照规律,表格中a= ,b= ,c= .
(2)观察表中规律,第n个“正方形数”是 ;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是 .
【答案】(1)见解析(2)见解析
【解析】
(1)首先根据前6个“三角形数”分别是1=![]() 、3=
、3=![]() 、6=
、6=![]() 、10=
、10=![]() 、15=
、15=![]() 、21=
、21=![]() ,可得第n个“三角形数”是
,可得第n个“三角形数”是![]() ,据此求出a的值是多少;然后根据前5个“正方形数”分别是1=12,4=22,9=32,16=42,25=52,可得第n个“正方形数”是n2,据此求出b的值是多少;最后根据前4个“五边形数”分别是1=
,据此求出a的值是多少;然后根据前5个“正方形数”分别是1=12,4=22,9=32,16=42,25=52,可得第n个“正方形数”是n2,据此求出b的值是多少;最后根据前4个“五边形数”分别是1=![]() ,5=
,5=![]() ,12=
,12=![]() ,22=
,22=![]() ,可得第n个“五边形数”是
,可得第n个“五边形数”是![]() ,据此求出c的值是多少即可.
,据此求出c的值是多少即可.
(2)首先判断出第n个“正方形数”是n2;然后分别求出第1个“三角形数”、第1个“正方形数”的和与第1个“五边形数”的差是多少,第2个“三角形数”、第2个“正方形数”的和与第2个“五边形数”的差是多少;第3个“三角形数”、第3个“正方形数”的和与第3个“五边形数”的差是多少;最后总结出规律,用含x、n的代数式表示第n个“五边形数”即可.
(1)∵前6个“三角形数”分别是:
1=![]() 、3=
、3=![]() 、6=
、6=![]() 、10=
、10=![]() 、15=
、15=![]() 、21=
、21=![]() ,
,
∴第n个“三角形数”是![]() ,
,
∴a=![]() =28.
=28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“正方形数”分别是:
1=![]() ,5=
,5=![]() ,12=
,12=![]() ,22=
,22=![]() ,
,
∴第n个“五边形数”是![]() ,
,
∴c=![]() =35.
=35.
(2)第n个“正方形数”是n2;
1+1-1=1,
3+4-5=2,
6+9-12=3,
10+16-22=4,
…,
∴第n个“五边形数”是n2+x-n.
故答案为:28、36、35;n2、n2+x-n.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时. 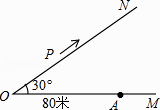
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y= ![]() 和y=
和y= ![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= ![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y= ![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= ![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( ) 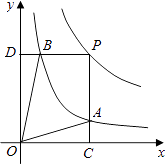
A.①②③
B.②③④
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=--![]() x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com