
【题目】如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD= ![]() ,则AD= .
,则AD= . 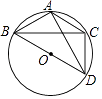
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() .以
.以 ![]() 为直径的
为直径的 ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() 是
是 ![]() 上一点,且
上一点,且 ![]() ,连接
,连接 ![]() ,过点
,过点 ![]() 作
作 ![]() ,交
,交 ![]() 的延长线于点
的延长线于点 ![]() ,则
,则 ![]() 的度数为( )
的度数为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
(3)结论应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
(4)能力提高:
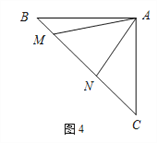
如图4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,试求出MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→ 食指的顺序,依次数整数 1,2,3,4,5,6,7,,当数到 2019 时,对应的手指为________________; 当第 n 次数到食指时,数到的数是_________________________ (用含 n 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
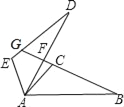
【题目】如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=∠AED=105°,∠CAD=10°,∠B=∠D=25°,求∠DFB、∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
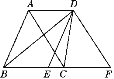
【题目】如图,在封闭图形ABCD中,AD∥BC,且AD=4,三角形ABC的周长为14,将三角形ABC平移到三角形DEF的位置.
(1)指出平移的方向和平移的距离;
(2)求封闭图形ABFD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com