
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )

A. ①②④ B. ①②③ C. ①④ D. ③④
【答案】C
【解析】①由抛物线与x轴的两交点坐标可求出抛物线的对称轴为x=1,进而即可得出2a+b=0,①符合题意;②结合图形即可得出当﹣1≤x≤3时,y≤0,②不符合题意;③根据二次函数的性质找出:当x≤1时,y值随x的增大而减小,进而即可得出③不符合题意;④由(3,0)在抛物线上,代入后即可得出9a+3b+c=0,④符合题意.综上即可得出结论.(只需分析①②利用排除法即可得出结论)
解:①∵抛物线与x轴的交点坐标为(﹣1,0)、(3,0),
∴抛物线的对称轴为x=﹣![]() =
=![]() =1,
=1,
∴b=﹣2a,即2a+b=0,①符合题意;
②∵抛物线与x轴的交点坐标为(﹣1,0)、(3,0),且抛物线开口向上,
∴当﹣1≤x≤3时,y≤0,②不符合题意;
③∵抛物线的对称轴为x=1,且开口向上,
∴当x≤1时,y值随x的增大而减小,
∴当x1<x2≤1时,y1>y2,③不符合题意;
④当x=3时,y=9a+3b+c=0,
∴9a+3b+c=0,④符合题意.
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】请把下列的证明过程补充完整:

已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE.
证明:∵AB∥CD(已知)
∴∠4=∠______
∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠______
∴∠3=∠______(等量代换)
∴AD∥BE______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,重庆一中初三(1)班数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计我校11000名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
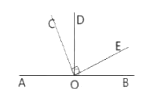
【题目】如图,过直线![]() 上一点
上一点![]() ,作
,作![]() ,
,![]() ,若
,若![]() ,①你还能求出哪些角的度数_____________________(至少写出两个,直角和平角除外);
,①你还能求出哪些角的度数_____________________(至少写出两个,直角和平角除外);
②与![]() 互余的角有__________,它们的数量关系是________;由此你得出的结论是_____________________.
互余的角有__________,它们的数量关系是________;由此你得出的结论是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
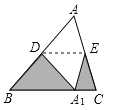
【题目】如图,三角形ABC的面积为1,将三角形ABC沿着过AB的中点D的直线折叠,使点A落在BC边上的![]() 处,折痕为DE,若此时点E是AC的中点,则图中阴影部分的面积为______________.
处,折痕为DE,若此时点E是AC的中点,则图中阴影部分的面积为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角三角形ABC中,∠ABC=90,将三角形ABC绕着点B逆时针旋转一定角度得到三角形BEF,EF交BC于点G.

(1)若![]() ,当∠ABE等于多少度时,
,当∠ABE等于多少度时,![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,
①求BG的长;
②连接AF交BE于点O,连接AE(如图2),设三角形EOF的面积为m,求三角形AEO的面积(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长度;
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜测出MN的长度吗?请说出你发现的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com