
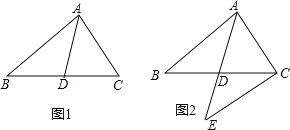
【题目】在△ABC中,D是边BC的中点.
(1)①如图1,求证:△ABD和△ACD的面积相等;
②如图2,延长AD至E,使DE=AD,连结CE,求证:AB=EC.
(2)当∠BAC=90°时,可以结合利用以上各题的结论,解决下列问题:
①求证:AD![]() BC(即:直角三角形斜边上的中线等于斜边的一半);
BC(即:直角三角形斜边上的中线等于斜边的一半);
②已知BC=4,将△ABD沿AD所在直线翻折,得到△ADB',若△ADB'与△ABC重合部分的面积等于△ABC面积的![]() ,请画出图形(草图)并求出AC的长度.
,请画出图形(草图)并求出AC的长度.
【答案】(1)①证明见解析;②证明见解析;(2)①证明见解析;②作图见解析,AC=2或2![]() .
.
【解析】
(1)①作△ABC,AB边上的高,根据三角形面积公式即可得出结论;
②证明△ABD≌△ECD,即可证明AB=EC;
(2)①根据△ABD≌△ECD可得AD=DE=![]() ,再证△ABC≌△CEA可得BC=AE,由此可得结论;
,再证△ABC≌△CEA可得BC=AE,由此可得结论;
②分AB>AC,AB<AC,AB=AC三种情况讨论,画出对应图,运用分类讨论的数学思想,逐一分类解析,即可解决问题.
解:(1)①过点A作AH⊥BC,垂足为H,
则S△ABD![]() BDAH,S△ACD
BDAH,S△ACD![]() CDAH.
CDAH.
∵点D是BC中点,
∴BD=CD,
∴△ABD和△ACD的面积相等.
②在△ABD和△ECD中,
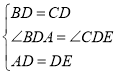 ,
,
∴△ABD≌△ECD(SAS),
∴AB=EC.
(2)①∵△ABD≌△ECD(已证),
∴∠B=∠ECD;
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=∠BAC=90°;
在△ABC与△CEA中,
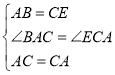 ,
,
∴△ABC≌△CEA(SAS),
∴BC=AE;
∵AD![]() AE,∴AD
AE,∴AD![]() BC.
BC.
②画草图如下:
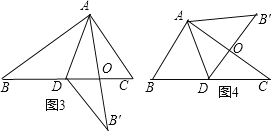
(Ⅰ)当AB>AC时,如图3,由△ADB'与△ABC重合部分的面积等于△ABC面积的![]() ,
,
结合(1)①题的结论,可以得到点O既即是ABˊ的中点,也是CD的中点,
故四边形ADB'C为平行四边形,
∴AC=BˊD=BD![]() BC=2.
BC=2.
(Ⅱ)当AB<AC时,
如图4,类比(Ⅰ)可得OA=OC,OB’=OD,
又∵∠AO B’=∠DOC,
∴△AOBˊ≌△COD(SAS),
∴ABˊ=CD=2,∠Bˊ=∠CDO,
又∵∠Bˊ=∠B,
∴∠B=∠CDO,/span>
∴AB∥OD,
∴∠COD=∠BAC=90°,
又∵DO=OBˊ=1,
由勾股定理可得CO![]() ,
,
∴AC=2CO![]() .
.
(Ⅲ)当 AB=AC时,由等腰三角形的性质可知,
折叠后重合的面积等于△ABC面积的![]() ,
,
不可能等于![]() ,所以不合题意,舍去.
,所以不合题意,舍去.
综上所述:AC=2或2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O 的直径,点D在⊙O 上(点D不与A,B重合),直线AD交过点B的切线于点C,过点D作⊙O 的切线DE交BC于点E.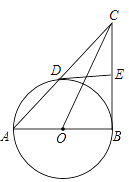
(1)求证:BE=CE;
(2)若DE平行AB,求sin∠ACO 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
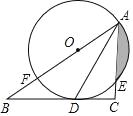
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课余生活,拓展学生的视野,某学校开设了特色选修课程.本学期该校共开设A、B、C三类课程,如下表所示.

(1)若小明从A类课程中随机选择一门课程,则他恰好选中“合唱”的概率是 .
(2)若小明分别从B类课程和C类课程中各随机选择一门课程,求他恰好选中“汉字的故事”和“乒乓球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
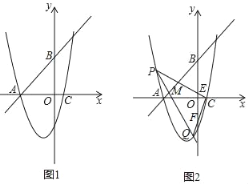
【题目】已知直线y=x+4分别交x轴、y轴于A、B两点,抛物线y=x2+mx﹣4经过点A,和x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;
(3)如图2,经过点M(﹣4,1)的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求OEOF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com