练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     (－)0－＋．


    解：原式=1－(2－1) +2+ (2－)

    =1－1+2+2－                             

    =+2                                                                                              


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    四边形ABCD是矩形，点P是直线AD与BC外的任意一点，连接PA、PB、PC、PD．请解答下列问题：

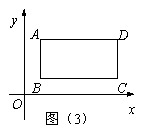
    （1）如图（1），当点P在线段BC的垂直平分线MN上（对角线AC与BD的交点Q除外）时，证明△PAC≌△PDB；

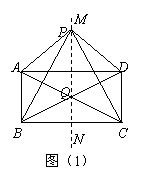
    （2）如图（2），当点P在矩形ABCD内部时，求证：PA2+PC2=PB2+PD2；

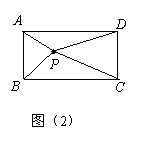
    （3）若矩形ABCD在平面直角坐标系xoy中，点B的坐标为（1，1），点D的坐标为（5，3），如图（3）所示，设△PBC的面积为y，△PAD的面积为x，求y与x之间的函数关系式．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    抛物线y=2（x﹣3）2+1的顶点坐标是（　　）

    A．（3，1）   B．（3，﹣1）   C．（﹣3，1）  D．（﹣3，﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是（    ）

    A．m+3　　　　B．m+6   

    C．2m+3    D．2m+6

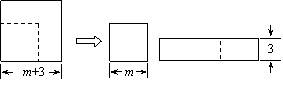
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    要使分式有意义，则x的取值范围是           

    查看答案和解析>>

    科目：初中数学 来源： 题型：


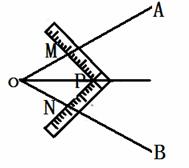
    我校八（1）班同学上数学活动课，利用角尺平分一个角（如图）.设计了如下方案：                        

    （Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线.

    （Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线.

    （1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由.

    （2）在方案（Ⅰ）PM=PN的情况下，继续移动角尺，同时使PM⊥OA，PN⊥OB.此方案是否可行？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在Rt△ABC中，∠C=90°，AB=5，BC=3，以AC所在的直线为轴旋转一周，所得圆锥的侧面积为（  ）

    A．12π          B．15π              C．24π        D．30π

    查看答案和解析>>

    科目：初中数学 来源： 题型：


                  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列图形是几家电信公司的标志，其中既是轴对称图形又是中心对称图形的是（  ）

     


    查看答案和解析>>

    同步练习册答案