
如图1,Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D在边AB的延长线上,BD=3,过点D作DE⊥AB,与 边AC的延长线相交于点E,以DE为直径作⊙O交AE于点F.
边AC的延长线相交于点E,以DE为直径作⊙O交AE于点F.
(1)求⊙O的半径及圆心O到弦EF的距离;
(2)连接CD,交⊙O于点G(如图2).求证:点G是CD的中点.

解:(1)∵∠ACB=90°,AB=5,BC=3,由勾股定理得:AC=4,
∵AB=5,BD=3,
∴AD=8,
∵∠ACB=90°,DE⊥AD,
∴∠ACB=∠ADE,
∵∠A=∠A,
∴△ACB∽△ADE,
∴ =
= =
=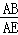
∴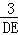 =
=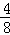 =
=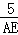
∴DE=6,AE=10,
即⊙O的半径为3;
过O作OQ⊥EF于Q,
则∠EQO=∠ADE=90°,
∵∠QEO=∠AED,
∴△EQO∽△EDA,
∴ =
= ,
,
∴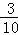 =
= ,
,
∴OQ=2.4,
即圆心O到弦EF的距离是2.4;…………5分
(2)连接EG,
∵AE=10,AC=4,
∴CE=6,
∴CE=DE=6,
∵DE为直径,
∴∠EGD=90°,
∴EG⊥CD,
∴点G为CD的中点.…………9分



 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;
(1)取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图27229(2)中阴影部分,求正六角星形A1F1B1D1C1E1的面积;
(2)取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图27229(3)中阴影部分,求正六角星形A2F2B2D2C2E2的面积.
(3) 取△A2B2C2和△D2E2F2各边中点,连接成正六角星形A3F3B3D3C3E3,依此法进行下去,试推测正六角星形AnFnBnDnCnEn的面积.

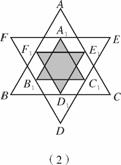

图27229
查看答案和解析>>
科目:初中数学 来源: 题型:
某粮食公司需要把2400吨大米调往灾区救灾.
(1)调动所需时间t(单位:天)与调动速度v(单位:吨/天)有怎样的函数关系?
(2)公司有20辆汽车,每辆汽车每天可运输6吨,预计这批大米最快在几天内全部运到灾区?
查看答案和解析>>
科目:初中数学 来源: 题型:
方程(k2-4)x2+(k+2)x+(k-6)y=k+8是关于x,y的方程,试问当k为何值时:(1)方程为一元一次方程? (2)方程为二元一次方程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com