
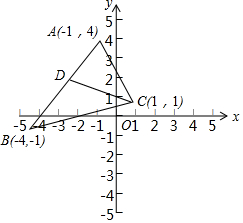 如图,△ABC的三个顶点坐标分别为A(-1,4)、B(-4.-1)、C(1,1),点D为AB的中点.
如图,△ABC的三个顶点坐标分别为A(-1,4)、B(-4.-1)、C(1,1),点D为AB的中点.分析 ①直接根据中点坐标公式即可得出D点坐标;
②利用待定系数法即可得出直线CD的解析式.
解答 解:①∵A(-1,4)、B(-4,-1),点D为AB的中点,
∴D($\frac{-1-4}{2}$,$\frac{4-1}{2}$),即D(-$\frac{5}{2}$,$\frac{3}{2}$);
②设直线CD的解析式为y=kx+b(k≠0),
∵C(1,1),D(-$\frac{5}{2}$,$\frac{3}{2}$),
∴$\left\{\begin{array}{l}{k+b=1}\\{-\frac{5}{2}k+b=\frac{3}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{7}}\\{b=\frac{8}{7}}\end{array}\right.$,
∴直线CD的解析式为:y=-$\frac{1}{7}$x+$\frac{8}{7}$.
点评 本题考查的是利用待定系数法求一次函数的解析式,熟知待定系数法求一次函数解析式一般步骤是解答此题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
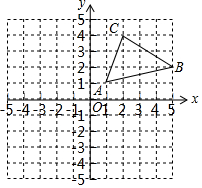 已知如图,△ABC的顶点均在格点上,点C的坐标是(2,4).
已知如图,△ABC的顶点均在格点上,点C的坐标是(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
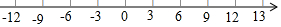 如图,点A从原点出发向数轴负方向运动,同时点B也从原点出发向数轴正方向运动,3秒后,A,B两点相距15个单位长度.已知点A与点B的速度之比是1:4(速度单位:长度/秒).
如图,点A从原点出发向数轴负方向运动,同时点B也从原点出发向数轴正方向运动,3秒后,A,B两点相距15个单位长度.已知点A与点B的速度之比是1:4(速度单位:长度/秒).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 模球次数 | 15 | 80 | 180 | 600 | 1000 |
| 模到白球次数 | 5 | 21 | 39 | 250 | |
| 模到白球的频率 | 0.33 | 0.26 | 0.21 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
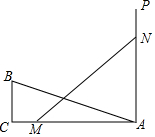 如图,Rt△ABC中,∠C=90°,BC=2,一条直线MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动.问点M运动到什么位置,才能使△ABC和△AMN全等?并证明你的结论.
如图,Rt△ABC中,∠C=90°,BC=2,一条直线MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动.问点M运动到什么位置,才能使△ABC和△AMN全等?并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com