
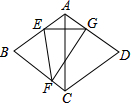
 如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( )
如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( )| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 4$\sqrt{6}$ | D. | 6 |
分析 如图,设AC与EG交于点O,FG交AC于H.只要证明FG⊥AD,即可FG是菱形的高,求出FG即可解决问题.
解答 解:如图,设AC与EG交于点O,FG交AC于H.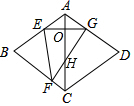
∵四边形ABCD是菱形,∠BAD=120°,
易证△ABC、△ACD是等边三角形,
∴∠CAD=∠B=60°,
∵EG⊥AC,
∴∠GOH=90°,
∵∠EGF=∠B=60°,
∴∠OHG=30°,
∴∠AGH=90°,
∴FG⊥AD,
∴FG是菱形的高,即等边三角形△ABC的高=$\frac{\sqrt{3}}{2}$×8=4$\sqrt{3}$.
故答案为4$\sqrt{3}$.
点评 本题考查翻折变换、等边三角形的判定和性质等知识,解题的关键是证明线段FG是菱形的高,记住等边三角形的高=$\frac{\sqrt{3}}{2}$a(a是等边三角形的边长),属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
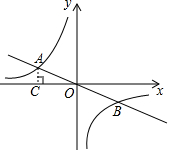 如图,双曲线y=$\frac{k}{x}$(k≠0)和直线y=$-\frac{1}{3}x$在第二、四象限分别交于A,B,过点A作AC⊥x轴于点C.已知点B的横坐标为3.
如图,双曲线y=$\frac{k}{x}$(k≠0)和直线y=$-\frac{1}{3}x$在第二、四象限分别交于A,B,过点A作AC⊥x轴于点C.已知点B的横坐标为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
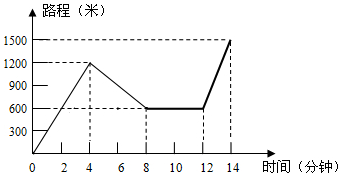 小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
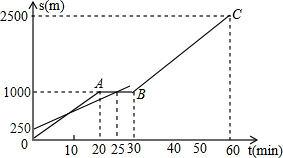 小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
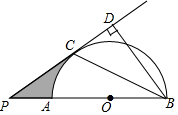 如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC
如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com