
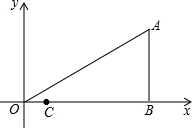
 如图,在平面直角坐标系中,已知Rt△ABO的顶点B在x轴正半轴上,∠AOB=30?,OA=2$\sqrt{3}$,C($\frac{1}{2}$,0),P 为OA上的一个动点,
如图,在平面直角坐标系中,已知Rt△ABO的顶点B在x轴正半轴上,∠AOB=30?,OA=2$\sqrt{3}$,C($\frac{1}{2}$,0),P 为OA上的一个动点,分析 (1)根据直角三角形30度角性质以及勾股定理求出OB、AB即可.
(2)作B关于直线OA的对称点B′,连接B′C交OA于点P,此时PC+PB最小,连接OB′.求出点B′坐标,利用两点间距离公式计算即可.
解答 解:(1)在Rt△AOB中,
∵∠AOB=30°,OA=2$\sqrt{3}$,∠ABO=90°,
∴AB=$\frac{1}{2}$OA=$\sqrt{3}$,
∴OB=$\sqrt{O{A}^{2}-A{B}^{2}}$=3,
∴A(3,$\sqrt{3}$).
(2)作B关于直线OA的对称点B′,连接B′C交OA于点P,此时PC+PB最小,连接OB′.
∵OB=OB′,∠BOB′=2∠AOB=60°,
∴△BOB′是等边三角形,易知B′($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),
∵PB=PB′,
∴PB+PC=PC+PB′=CB′=$\sqrt{(\frac{3}{2}-\frac{1}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{31}}{2}$,
∴PB+PC的最小值为$\frac{\sqrt{31}}{2}$.
点评 本题考查轴对称-最短问题、坐标与图形、直角三角形30度角性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
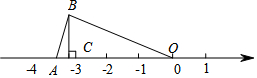 如图,OA=OB,BC=1,则数轴上点A所表示的数为( )
如图,OA=OB,BC=1,则数轴上点A所表示的数为( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $-\sqrt{10}$ | D. | -3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2003年农村居民人均收入低于2002年 | |
| B. | 农村居民人均收入年增长率低于9%的有2年 | |
| C. | 农村居民人均收入最多的是2004年 | |
| D. | 农村居民人均收入在逐年增加 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
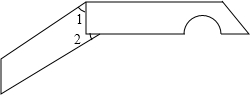 如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.
如图,是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com