
【题目】某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.

(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
【答案】解:(1)设y与x之间的函数关系式为y=kx+b,由函数图象,得
![]() ,解得:
,解得:![]() 。
。
∴y与x之间的函数关系式为y=﹣x+300。
(2)∵y=﹣x+300,∴当x=120时,y=180。
设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,由题意,得
120a+180×2a=7200,解得:a=15,
∴乙品牌的进货单价是30元。
答:甲、乙两种品牌的文具盒进货单价分别为15元,30元。
(3)设甲品牌进货m个,则乙品牌的进货(﹣m+300)个,由题意,得
![]() ,解得:180≤m≤181。
,解得:180≤m≤181。
∵m为整数,∴m=180,181。
∴共有两种进货方案:
方案1:甲品牌进货180个,则乙品牌的进货120个;
方案2:甲品牌进货181个,则乙品牌的进货119个。
设两种品牌的文具盒全部售出后获得的利润为W元,由题意,得
W=4m+9(﹣m+300)=﹣5m+2700。
∵k=﹣5<0,∴W随m的增大而减小。
∴m=180时,W最大=1800元。
【解析】
(1)根据函数图象由待定系数法就可以直接求出y与x之间的函数关系式;
(2)设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,根据购进甲品牌文具盒120个可以求出乙品牌的文具盒的个数,由购进两种品牌的文具盒其需7200元建立方程即可求出a值;
(3)设甲品牌进货m个,则乙品牌进货(300-m)个,根据条件建立不等式组求出满足条件的解即可.


科目:初中数学 来源: 题型:
【题目】用黑、白正方形按如图规律排列.

(1)第10个和第11图形中,黑色正方形各有多少个?
(2)找出图形变化的规律,说明第n个图形中黑色正方形的个数与n的关系.
(3)这列图形中,是否存在黑色正方形的个数为2019的图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b、c在数轴上的位置如图:
![]()
(1)用不等号填空:-b 0,|c| 0,|a| |b|,b-c 0,a+b 0,c-a 0.
(2)化简:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
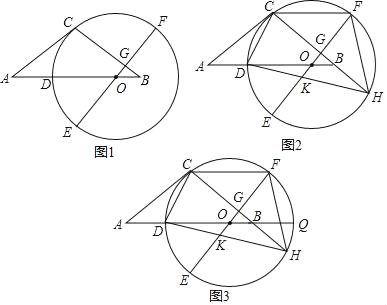
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆与AC相切于点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G.
(1)求证:D是弧EC的中点;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点K,连接CF,求证:CF=OK+DO;
(3)如图3,在(2)的条件下,延长DB交⊙O于点Q,连接QH,若DO=![]() ,KG=2,求QH.
,KG=2,求QH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,抛物线y=ax2+bx+3与x轴交于点B、C,与y轴交于点A,且AO=CO,BC=4.
(1)求抛物线解析式;
(2)如图2,点P是抛物线第一象限上一点,连接PB交y轴于点Q,设点P的横坐标为t,线段OQ长为d,求d与t之间的函数关系式;
(3)在(2)的条件下,过点Q作直线l⊥y轴,在l上取一点M(点M在第二象限),连接AM,使AM=PQ,连接CP并延长CP交y轴于点K,过点P作PN⊥l于点N,连接KN、CN、CM.若∠MCN+∠NKQ=45°时,求t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
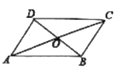
(1)求证:四边形ABCD是平行四边形
(2)若AC⊥BD,且AB=4,则四边形ABCD的周长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com