
已知矩形纸片ABCD中,AB=1,BC=2,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A,处,给出以下判断:
(1)当四边形A,CDF为正方形时,EF=
(2)当EF= 时,四边形A,CDF为正方形
时,四边形A,CDF为正方形
(3)当EF= 时,四边形BA,CD为等腰梯形;
时,四边形BA,CD为等腰梯形;
(4)当四边形BA,CD为等腰梯形时,EF= 。
。
其中正确的是 (把所有正确结论序号都填在横线上)。
(1)(3)(4)
解析试题分析:(1)依题意知,当四边形A,CDF为正方形时,
则A’C=CD=1,则B A’="BC-" A’C=1.故四边形AB A’F也为正方形。故E点落在B点上。
则EF为正方形对角线,故EF= 正确。
正确。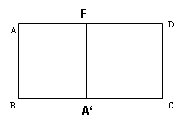
(2)如图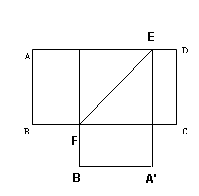 ,
,
在AD上任意截取一段长度为1的线段,并从两个端点向BC做垂线得到一个正方形,其中EF为其对角线,则EF= ,但四边形A,CDF却不是正方形。故错误。
,但四边形A,CDF却不是正方形。故错误。
(3)
依题意知当EF= 时,即EF与BD重叠,为长方形ABCD的对角线。此时,BA’=CD。故四边形BA,CD为等腰梯形;
时,即EF与BD重叠,为长方形ABCD的对角线。此时,BA’=CD。故四边形BA,CD为等腰梯形;
(4)
当四边形BA,CD为等腰梯形时,则BA’="CD" ,可知图形沿着BD折叠,故EF=BD= 。
。
考点:折叠性质
点评:本题难度中等,主要考查学生对折叠性质知识点的掌握,为中考常考题型,要求学生注意数形结合应用。


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
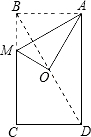 如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为
如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com