
����Ŀ��ij�ľߵ�������A��B�����ͺŵ������50���������ۣ���������Ľ��ۡ��ۼ����±���ʾ��
����ͺ� | ���ۣ�Ԫ/���� | �ۼۣ�Ԫ/���� |
A�� | 200 | 300 |
B�� | 100 | 150 |
������50��������ܷ��ò�����7300Ԫ���ҹ���B������ĸ���������A�����������![]() ��
��
��1�����ľߵ����ļ��ֽ���������
��2�������ľߵ깺����50�����ȫ�����꣬����ľߵ�������ֽ������������ܻ�����������������Ƕ��٣��������ۼ۩����ۣ�
���𰸡���1����4�ֽ����������ֱ��ǣ���A��20����B��30������A��21����B��29������A��22����B28������A��23����B27������2������A��23����B��27����������������Ϊ3650Ԫ��
��������
��1���蹺��A�����x������B�ͣ�50��x������������ù���x�IJ���ʽ�飬���x�ķ�Χ���ٸ���xΪ���������ɵ�x����50��x����ֵ������������ɵã�
��2�������yԪ������������ڣ�A���ۼ۩����ۣ���A�Ĺ�������+��B���ۼ۩����ۣ���B�Ĺ����������г�������ϵʽ������һ�κ��������ʿɵô𰸣�
�⣺��1���蹺��A�����x������B�ͣ�50��x������
������ã�  ��
��
��ã�20��x��23��
��A��������Թ���20��21��22��23����B��������Թ�����50��x��������30��29��28��27����
����4�ֽ����������ֱ��ǣ���A��20����B��30������A��21����B��29������A��22����B28������A��23����B27����
��2�������yԪ��������ã�
y����300��200��x+��150��100����50��x��
��100x+50��50��x��
��50x+2500��
��50��0��
��y��x�����������
�൱x��23ʱ��y���y���ֵ��50��23+2500��3650��
�𣺹���A��23����B��27����������������Ϊ3650Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=6cm��AD=8cm����P�ӵ�B�������ضԽ���BD���D�����˶����ٶ�Ϊ4cm/s������P��PQ��BD��BC�ڵ�Q����PQΪһ����������PQMN��ʹ�õ�N��������PD�ϣ���O�ӵ�D��������DC���C�����˶����ٶ�Ϊ3cm/s����OΪԲ�ģ�1cm�뾶����O����P���Dͬʱ�����������ǵ��˶�ʱ��Ϊt����λ��s�� ��0��t��![]() ����
����
��1����ͼ1������DQ����DQƽ�֡�BDC����t��ֵΪ�� ��s��
��2����ͼ2������CM�����CMQ�����ΪS����S����t�ĺ�����ϵʽ��
��3�����˶������У���tΪ��ֵʱ����O��MN��һ�����У�
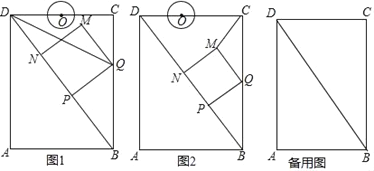
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽��֤����
(1)ij����ѧ����ѧϰС��Ծ������������ഹֱ���߶���������ڱߵ�������ϵ����̽��������������⣬�������֤����
��ͼ�٣��ھ���ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H.��֤�� ![]() ��
��
������Ӧ�á�
(2)��ͼ�ڣ�������(1)�������£���AM��BN����M��N�ֱ��ڱ�BC��CD�ϣ���![]() ����
����![]() ��ֵΪ ��
��ֵΪ ��
����ϵ��չ��
(3)��ͼ�ۣ��ı���ABCD�У���ABC=90����AB=AD=10��BC=CD=5��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���![]() ��ֵ��
��ֵ��
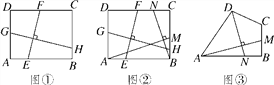
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���2���Խ���AC��BD�ཻ�ڵ�O����E��F�ֱ��ڱ�AD��AB�ϣ���OE��OF�����ı���AFOE������ǣ�������

A.4B.2C.1D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����E��F�ֱ���CD��BC���е㣬AE��DF���ڵ�P������CP����CP��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=2x+2��y�ύ��A�㣬�뷴��������y=![]() ��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO=2��
��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO=2��
��1����k��ֵ��
��2����N��a��1���Ƿ���������y=![]() ��x��0��ͼ���ϵĵ㣬��x�����Ƿ���ڵ�P��ʹ��PM+PN��С�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��x��0��ͼ���ϵĵ㣬��x�����Ƿ���ڵ�P��ʹ��PM+PN��С�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�ڣ�OΪԭ�㣬��A������Ϊ(10��0)����B�ڵ�һ�����ڣ�BO��5��sin��BOA��![]() . ��(1)��B�����ꣻ(2)cos��BAO��ֵ��
. ��(1)��B�����ꣻ(2)cos��BAO��ֵ��
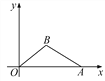
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳��
��ͼ1����֪��![]() ��������
��������![]() �������Խ��ߵĽ��㣬�Ե�
�������Խ��ߵĽ��㣬�Ե�![]() Ϊֱ�Ƕ����ֱ��������
Ϊֱ�Ƕ����ֱ��������![]() ������
������![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��

��1��![]() �ij���Ϊ________��
�ij���Ϊ________��
����֤����
��2����ͼ2���ڣ�1���������£���![]() ����ͼ���ã���
����ͼ���ã���![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() �����ж�
�����ж�![]() ��
��![]() ��������������ϵ����֤�����ۣ�
��������������ϵ����֤�����ۣ�

̽�����֣�
��3����ͼ3���ڣ�1���������£���![]() ����ͼ���ã�����
����ͼ���ã�����![]() ǡ����
ǡ����![]() �ϣ���֤��
�ϣ���֤��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ��������Σ�AB��AC���ֱ�������Ϊ�����ABC�����ȱ�������ADB�͵ȱ�������ACE�� ����DAE����DBC�����BAC�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com