Question

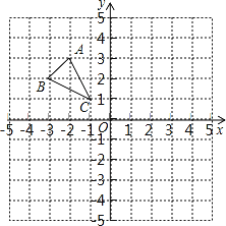
【题目】如图，△ABC的顶点分别为A（-2,3），B（-3,2），C（-1,1）

（1）画出△ABC关于y轴对称的△A1B1C1；

（2）请在x轴上确定一点D，使点D到B、C的距离相等（要求用直尺和圆规作图，并保留作图痕迹）

Answer 1

【答案】（1）图略；2）图略

【解析】试题分析：

（1）根据点A、B、C的坐标可得点A1、B1、C1的坐标，由此即可在图中描出表示点A1、B1、C1的点，顺次连接这三点即可得到所求三角形；

（2）根据“到线段两端距离相等的点在线段的垂直平分线上”，作线段BC的垂直平分线，所得直线与x轴的交点即为所求的点D.

试题解析：

（1）∵点A（-2,3），B（-3,2），C（-1,1）关于轴的对称点分别是点A1、B1、C1，

∴点A1、B1、C1的坐标分别是（2，3）、（3，2）、（1，1）.

由此可画出△A1B1C1如下图所示：

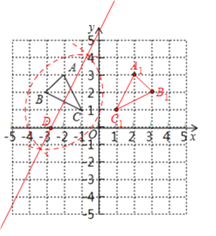
（2）如上图所示，作线段BC的垂直平分线，所作直线与x轴的交点即为所求的D点.