
 如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.
如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.| 2 |
| 2 |
| AC2+BC2 |
| 42+42 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 抛物线的对称轴为直线x=m.求当k为何值时,|m|=
抛物线的对称轴为直线x=m.求当k为何值时,|m|=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源:浙江省中考真题 题型:解答题

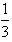 ?
?查看答案和解析>>
科目:初中数学 来源: 题型:
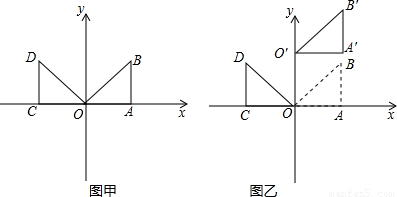
如图甲,在等腰直角三角形![]() 中,
中,![]() ,
, ![]() 点在第一象限,
点在第一象限,![]() 点坐标为
点坐标为![]() .
.![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)求经过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)若将![]() 向上平移
向上平移![]() 个单位至
个单位至![]() (如图乙),则经过
(如图乙),则经过![]() 三点的抛物线的对称轴在
三点的抛物线的对称轴在![]() 轴的 .(填“左侧”或“右侧”)
轴的 .(填“左侧”或“右侧”)
(3)在(2)的条件下,设过![]() 三点的抛物线的对称轴为直线
三点的抛物线的对称轴为直线![]() .求当
.求当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源:2008年浙江省湖州市中考数学试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:2012年苏教版初中数学八年级上5.1函数练习卷(解析版) 题型:选择题
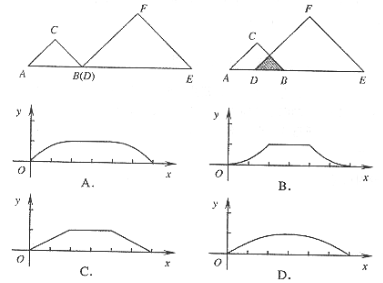
如图,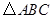 和的
和的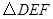 是等腰直角三形,
是等腰直角三形,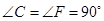 ,
,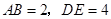 .点B与点D重合,点
.点B与点D重合,点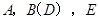 在同一条直线上,将
在同一条直线上,将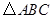 沿
沿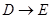 方向平移,至点
方向平移,至点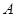 与点
与点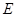 重合时停止.设点
重合时停止.设点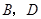 之间的距离为x,
之间的距离为x,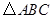 与
与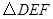 重叠部分的面积为
重叠部分的面积为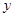 ,则准确反映
,则准确反映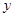 与
与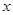 之间对应关系的图象是( )
之间对应关系的图象是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com