
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

【答案】(1)见解析;(2)OE=2.
【解析】
(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DAC,得出CD=AD=AB,即可得出结论;
(2)先判断出OE=OA=OC,再求出OB=1,利用勾股定理求出OA,即可得出结论.
解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=![]() BD=1,
BD=1,
在Rt△AOB中,AB=![]() ,OB=1,
,OB=1,
∴OA=![]() =2,
=2,
∴OE=OA=2.


科目:初中数学 来源: 题型:
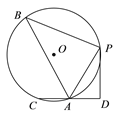
【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为绿化校园,安排七年级三个班植树,其中,一班植树x棵,二班植树的棵数是一班的2倍少20棵,三班植树的棵数是二班的一半多15棵.
(1)三个班共植树多少棵?(用含x的式子表示)
(2)当x=30时,三个班中哪个班植树最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为( )
A.1985B.-1985C.2019D.-2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(大丰某校数学兴趣小组活动场景)
(课堂再现)
师:同学们还记得教材P43分配律a(b+c)=ab+ac吗?现在,老师和大家一起来用几何的方法来证明这个公式。相信今天会惊喜不断。(学生期待惊喜中………),
(教者呈现教具)老师手上有两个长方形,长分别是b、c,宽都是a,(如图1)它们各自面积是多少?
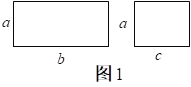

生1:面积分别为ab、ac。
师:现在我们把它们拼在一起(如图2),组成了一个新长方形,新长方形面积又是多少呢?
生2:![]()
师:所以……
生3:所以得到![]() ,也就是说
,也就是说![]() (真好玩!)
(真好玩!)
师:相信大家能用类似方法来推导一个我们暂时还没学习的公式,老师期待大家给我的惊喜哦!(屏幕上呈现问题)
(拓展延伸)
将边长为a的正方形纸板上剪去一个边长为b的正方形(如图3),将剩余的纸板沿虚线剪开,拼成如图4的梯形。

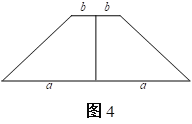
(1)你能得到一个什么等式.(用含a、b的式子表示)
(再接再厉)
(2)直接运用上面你发现的公式完成运算:![]()
(拓展提高)
(3)直接运用上面你发现的公式解下列方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)8÷(﹣2)2﹣4×(﹣3)﹣|﹣6|
(2)(![]() )×(﹣12)
)×(﹣12)
(3)(4x+2y)-3(x-2y)
(4)4ab2-3[a2b-2(a2b-2ab2)]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂车间为了了解工人日均生产能力的情况,随机抽取10名工人进行测试,将获得数据制成如下统计图.
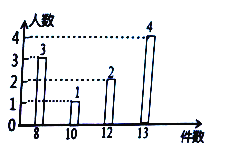
(1)求这10名工人的日均生产件数的平均数、众数、中位数;
(2)若日均生产件数不低于12件为优秀等级,该工厂车间共有工人120人,估计日均生产能力为“优秀”等级的工人约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
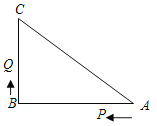
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com