
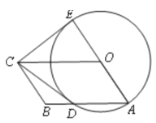
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程![]() 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
【答案】(1)、证明过程见解析;(2)、48.
【解析】
试题分析:(1)、连接OD,根据切线得出∠OEC=90°,根据OD=OA以及OC∥AD得出∠OAD=∠EOC,则∠EOC=∠DOC,结合OD=OE,OC=OC得出△ODC和△OEC全等,从而得出∠ODC=∠OEC=90°,得出切线;(2)、根据方程得出OC=10,OA=6,根据勾股定理得出CD=8,根据全等得出CE=8,然后计算四边形的面积.
试题解析:(1)、连OD,∵CE是⊙O的切线, ∠OEC=90O ,∵OD=OA,∴∠ODA=∠OAD,又∵OC//AD
∴∠OAD =∠EOC,∠DOC=∠ODA,∴∠EOC=∠DOC, 又∵OD=OE,OC=OC, ∴△ODC≌△OEC(SAS)
∴∠ODC=∠OEC=90 O, ∴CD是⊙O的切线。
(2)、![]() ,
,![]() ,即OC=10,OA=6 在Rt△ODC, CD=8 ∵△ODC≌△OEC ,CE=CD=8
,即OC=10,OA=6 在Rt△ODC, CD=8 ∵△ODC≌△OEC ,CE=CD=8
∴平行四边形OABC的面积S=OA×CE=6×8=48


科目:初中数学 来源: 题型:
【题目】以下问题不适合全面调查的是( )
A.调查某班学生每周课前预习的时间
B.调查某中学在职教师的身体健康状况
C.调查全国中小学生课外阅读情况
D.调查某校篮球队员的身高
查看答案和解析>>
科目:初中数学 来源: 题型:
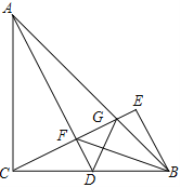
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD
求证:(1) △BEF为等腰直角三角形 ;(2) ∠ADC=∠BDG.
查看答案和解析>>
科目:初中数学 来源: 题型:
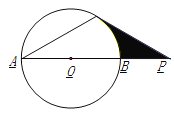
【题目】如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
(1) 求证:CP是⊙O的切线;
(2) 若PC=6,AB=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 平行四边形的对边相等 B. 四条边都相等的四边形是菱形
C. 矩形的两条对角线互相垂直 D. 等腰梯形的两条对角线相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com