
ЁОЬтФПЁПЪ§жсЪЧбЇЯАгаРэЪ§ЕФвЛжжживЊЙЄОпЃЌШЮКЮгаРэЪ§ЖМПЩвдгУЪ§жсЩЯЕФЕуБэЪОЃЌетбљФмЙЛдЫгУЪ§аЮНсКЯЕФЗНЗЈНтОівЛаЉЮЪЬт.
ШчЭМЃЌНЋвЛЬѕЪ§жсдкдЕуOКЭЕуBДІИїелвЛЯТЃЌЕУЕНвЛЬѕЁАелЯпЪ§жсЁБ.ЭМжаЕуAБэЪОЃ10ЃЌЕуBБэЪО10ЃЌЕуCБэЪО18ЃЌЮвУЧГЦЕуAКЭЕуCдкЪ§жсЩЯЯрОр28ИіГЄЖШЕЅЮЛ.ЖЏЕуPДгЕуAГіЗЂЃЌвд2ЕЅЮЛУыЕФЫйЖШбизХелЯпЪ§ГщЁБЕФе§ЗНЯђдЫЖЏЃЌДгЕуOдЫЖЏЕНЕуBЦкМфЫйЖШБфЮЊдРДЕФвЛАыЃЌжЎКѓСЂПЬЛжИДдЫйЃЛЭЌЪБЃЌЖЏЕуQДгЕуCГіЗЂЃЌвд1ЕЅЮЛУыЕФЫйЖШбизХЪ§жсЕФИКЗНЯђдЫЖЏЃЌДгЕуBдЫЖЏЕНЕуOЦкМфЫйЖШБфЮЊдРДЕФСНБЖЃЌжЎКѓвВСЂПЬЛжИДдЫй.ЕБЕуPЕНДяЕуCЪБЃЌСНЕуЖМЭЃЩЯдЖЖЏ.ЩшдЫЖЏЕФЪБМфЮЊ1Уы.ЮЪЃК
(1)tЃН2УыЪБЃЌЕуPдкЁАелЯпЪ§жсЁБЩЯЫљЖдгІЕФЪ§ЪЧ_______ЃЛЕуPЕНЕуQЕФОрРыЪЧ_____ЕЅЮЛГЄЖШЃЛ
(2)ЖЏЕуPДгЕу4дЫЖЏжСCЕуашвЊ_______УыЃЛ
(3)PЁЂQСНЕуЯргіЪБЃЌЧѓГіtЕФжЕКЭДЫЪБЯргіЕуMдкЁАелЯпЪ§жсЁБЩЯЫљЖдгІЕФЪ§ЃЛ
(4)ШчЙћЖЏЕуPЁЂOСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШгыQЁЂBСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШЯрЕШЃЌжБНгаДГіtЕФжЕ.

ЁОД№АИЁП(1)![]() (2)10 (3)
(2)10 (3)![]() ,
,![]() (4)2ЃЌ6.5ЃЌ11ЃЌ17
(4)2ЃЌ6.5ЃЌ11ЃЌ17
ЁОНтЮіЁП
(1)ИљОнЬтвтМЦЫуГі![]() УыЪБЫљдЫЖЏЕФГЄЖШМДПЩЃЌНјЖјЫуГіPЁЂQжЎМфЕФОрРыЃЛ
УыЪБЫљдЫЖЏЕФГЄЖШМДПЩЃЌНјЖјЫуГіPЁЂQжЎМфЕФОрРыЃЛ
(2)ДгЕу4ЕНCЕуашвЊОЙ§OBЩЯвЛЖЮОрРывдМАBCЕФГЄЃЌАбЫќУЧЫљашЪБМфЯрМгМДПЩЃЛ
(3)ИљОнЯргіЕФЪБКђСНЕуЫљдЫЖЏЕФТЗГЬ=28ЃЌПЩвдСаГіЗНГЬЃЌНтГіtЕФжЕМДПЩ;
(4)ИљОнВЛЭЌЕФЧщПіНјааЬжТлМДПЩЃЌЗжЮЊ4жжЧщПіНтГіtжЕ.
НтЃК
(1)ЕБ![]() УыЪБЃЌЕуPдЫЖЏСЫ4ЃЌДЫЪБЖдгІЕФЪ§ЮЊЃК
УыЪБЃЌЕуPдЫЖЏСЫ4ЃЌДЫЪБЖдгІЕФЪ§ЮЊЃК![]() ЃЌ
ЃЌ
ЕуQдЫЖЏСЫ2ЃЌДЫЪБQЖдгІЕФЪ§ЮЊЃК![]() ЃЌ
ЃЌ
(2)![]() ЕуPЕНЕуQЕФОрРыЪЧ
ЕуPЕНЕуQЕФОрРыЪЧ![]() ЕЅЮЛГЄЖШ.
ЕЅЮЛГЄЖШ.
ДЫЪБЗжЮЊШ§ЖЮЃКPOЁЂOBЁЂBC,
ЕуPдкЕу4дЫЖЏЕНBЕуашвЊЪБМфЃК![]() (Уы)ЃЌ
(Уы)ЃЌ
ДгBЕНCашвЊЪБМфЃК![]() (Уы)ЃЌ
(Уы)ЃЌ
![]() вЛЙВашвЊЃК
вЛЙВашвЊЃК![]() (Уы)ЃЛ
(Уы)ЃЛ
(3)ОЗжЮіПЩЕУЯргівЛЖЈдкOBЩЯЃЌЩшОЙ§ЪБМфtСНепЯргіЃЌ
ДЫЪБдкOBЩЯЕуQЕФЪБМфЮЊЃК![]() ЃЌ
ЃЌ
дкOBЩЯЕуPЕФЪБМфЮЊЃК![]() ЃЌ
ЃЌ
ИљОнзмТЗГЬЮЊ28ЃЌСаГіЗНГЬЃК
![]()
НтЕУЃК![]() ЃЌ
ЃЌ
МДЃКОЙ§![]() УыЃЌPЁЂQСНЕуЯргіЃЌ
УыЃЌPЁЂQСНЕуЯргіЃЌ
ДЫЪБЖдгІЕФЪ§ЮЊЃК![]() .
.
(4)ЖЏЕуPЁЂOСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШгыQЁЂBСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШЯрЕШЃЌга4жжПЩФмЃК
ЂйЖЏЕуQдкCBЩЯЃЌЖЏЕуPдкAOЩЯЃЌ
дђЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() .
.
ЂкЖЏЕуQдкCBЩЯЃЌЖЏЕуPдкOBЩЯЃЌ
дђЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() .
.
ЂлЖЏЕуQдкBOЩЯЃЌЖЏЕуPдкOBЩЯЃЌ
дђЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() .
.
ЂмЖЏЕуQдкOAЩЯЃЌЖЏЕуPдкBCЩЯЃЌ
дђЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() .
.


 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЬнзгABППдкЧНЩЯЃЌЬнзгЕФЕзЖЫAЕНЧНИљOЕФОрРыЮЊ2mЃЌЬнзгЖЅЖЫBЕНЕиУцОрРыЮЊ7mЃЌЯжНЋЬнзгЕФЕзЖЫAЯђЭтвЦЖЏЕНAЁфЃЌЪЙЬнзгЕФЕзЖЫAЁфЕНЧНИљOЕФОрРыЕШгк4mЃЌЭЌЪБЬнзгЕФЖЅЖЫBЯТНЕжСBЁфЃЌФЧУДBBЁфЕФГЄЮЊЃЈЁЁЁЁЃЉ

A. ЕШгк1mB. Дѓгк1mC. аЁгк1mD. вдЩЯД№АИЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїAOBжаЃЌABЁЭOBЃЌЧвAB=OB=3ЃЌЩшжБЯп![]() НиДЫШ§НЧаЮЫљЕУвѕгАВПЗжЕФУцЛ§ЮЊSЃЌдђSгыtжЎМфЕФКЏЪ§ЙиЯЕЕФЭМЯѓЮЊЯТСабЁЯюжаЕФЃЈЁЁЁЁЃЉ
НиДЫШ§НЧаЮЫљЕУвѕгАВПЗжЕФУцЛ§ЮЊSЃЌдђSгыtжЎМфЕФКЏЪ§ЙиЯЕЕФЭМЯѓЮЊЯТСабЁЯюжаЕФЃЈЁЁЁЁЃЉ

A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
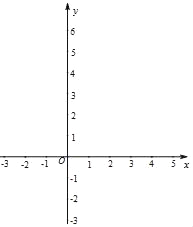
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2Љ4ax+3aЃЈaЃО0ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈAдкBЕФзѓВрЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФЖдГЦжсМАЕуAЃЌBЕФзјБъЃЛ
ЃЈ2ЃЉЕуCЃЈtЃЌ3ЃЉЪЧХзЮяЯпy=ax2Љ4ax+3aЃЈaЃО0ЃЉЩЯвЛЕуЃЌЃЈЕуCдкЖдГЦжсЕФгвВрЃЉЃЌЙ§ЕуCзїxжсЕФДЙЯпЃЌДЙзуЮЊЕуDЃЎ
ЂйЕБCD=ADЪБЃЌЧѓДЫЪБХзЮяЯпЕФБэДяЪНЃЛ
ЂкЕБCDЃОADЪБЃЌЧѓtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЙКТђСЫвЛЬзАВОгаЭЩЬЦЗЗПЃЌЫћзМБИНЋЕиУцЦЬЩЯЕизЉЃЌЕиУцНсЙЙШчЭМЫљЪОЃЎЧыИљОнЭМжаЕФЪ§ОнЃЈЕЅЮЛЃКmЃЉЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉгУКЌxЁЂyЕФДњЪ§ЪНБэЪОЕиУцзмУцЛ§ЃЛ
ЃЈ2ЃЉШєx=5ЃЌy=![]() ЃЌЦЬ1m2ЕизЉЕФЦНОљЗбгУЮЊ80дЊЃЌФЧУДЦЬЕизЉЕФзмЗбгУЮЊЖрЩйдЊЃП
ЃЌЦЬ1m2ЕизЉЕФЦНОљЗбгУЮЊ80дЊЃЌФЧУДЦЬЕизЉЕФзмЗбгУЮЊЖрЩйдЊЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=30ЁуЃЌвдAЮЊдВаФЃЌШЮвтГЄЮЊАыОЖЛЛЁЗжБ№НЛABЁЂACгкЕуMКЭNЃЌдйЗжБ№вдMЁЂNЮЊдВаФЃЌДѓгк![]() MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНсAPВЂбгГЄНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌСЌНсAPВЂбгГЄНЛBCгкЕуDЃЌдђЯТСаЫЕЗЈжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
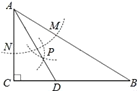
ЂйADЪЧЁЯBACЕФЦНЗжЯпЃЛЂкЁЯADC=60ЁуЃЛ ЂлЕуDдкABЕФжаДЙЯпЩЯЃЛЂмSЁїDACЃКSЁїABC=1ЃК3ЃЎ
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧхГЏЪ§бЇМвУЗЮФЖІЕФжјзїЁЖЗНГЬТлЁЗжагаетбљвЛЕРЬтЃКЩНЬяШ§ФЖЃЌГЁЕиСљФЖЃЌЙВелЪЕЬяЫФФЖЦпЗжЃЛгжЩНЬяЮхФЖЃЌГЁЕиШ§ФЖЃЌЙВелЪЕЬяЮхФЖЮхЗжЃЌЮЪУПФЖЩНЬяелЪЕЬяЖрЩйЃЌ
УПФЖГЁЕиелЪЕЬяЖрЩйЃП
выЮФЮЊЃКМйШчгаЩНЬя3ФЖЃЌГЁЕи6ФЖЃЌЦфВњСИЯрЕБгкЪЕЬя4.7ФЖЃЛгжЩНЬя5ФЖЃЌГЁЕи3ФЖЃЌЦфВњСИЯрЕБгкЪЕЬя5.5ФЖЃЌЮЪУПФЖЩНЬяКЭУПФЖГЁЕиВњСИИїЯрЕБгкЪЕЬяЖрЩйФЖЃПЧыФуНтД№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
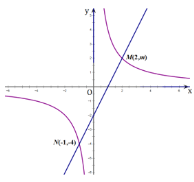
ЁОЬтФПЁПвЛДЮКЏЪ§![]() ЭМЯѓгыЗДБШР§КЏЪ§
ЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуMЁЂN.
ЕФЭМЯѓНЛгкЕуMЁЂN.
ЃЈ1ЃЉЧѓетСНИіКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓаДГіЪЙ![]() ЕФздБфСПЕФШЁжЕЗЖЮЇ.
ЕФздБфСПЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН![]() ЃЌADЃН2ЃЎЕуEЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЌСЌНгAEЃЌЙ§ЕуDзїDFЁЭAEгкЕуFЃЎЕБЁїCDFЪЧЕШбќШ§НЧаЮЪБЃЌBEЕФГЄЮЊ_____ЃЎ
ЃЌADЃН2ЃЎЕуEЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЌСЌНгAEЃЌЙ§ЕуDзїDFЁЭAEгкЕуFЃЎЕБЁїCDFЪЧЕШбќШ§НЧаЮЪБЃЌBEЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com