
【题目】定义:点![]() 是
是![]() 轴上一点,将函数
轴上一点,将函数![]() 的图象位于直线
的图象位于直线![]() 右侧部分,以
右侧部分,以![]() 轴为对称轴翻折,得到新的函数
轴为对称轴翻折,得到新的函数![]() 的图象,我们称函数
的图象,我们称函数![]() 是函数
是函数![]() 的相关函数,函数
的相关函数,函数![]() 的图象记作
的图象记作![]() ,函数
,函数![]() 的图象未翻折部分记作
的图象未翻折部分记作![]() ,图象
,图象![]() 和
和![]() 起来记作图象
起来记作图象![]() .
.
例如:函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的相关函数
时,它的相关函数![]() 的解析式为
的解析式为![]()
(1)如图,函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的相关函数
时,它的相关函数![]() 的解析式为_________;
的解析式为_________;
(2)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,图象
时,图象![]() 上某点的纵坐标为2,求该点的横坐标;
上某点的纵坐标为2,求该点的横坐标;
(3)函数![]() 的解析式为
的解析式为![]() ,
,
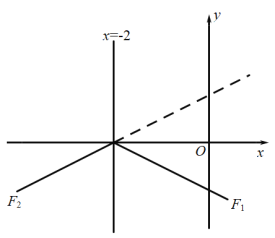
①已知点A、B的坐标分别为![]() 、
、![]() ,当
,当![]() 时,且图像
时,且图像![]() 与线段
与线段![]() 只有一个共点时,结合函数图象,求
只有一个共点时,结合函数图象,求![]() 的取值范围;
的取值范围;
②若![]() ,点
,点![]() 是图象
是图象![]() 上任意一点,当
上任意一点,当![]() 时,
时,![]() 的最大值始终保持不变,求
的最大值始终保持不变,求![]() 的取值范围(直接写出结果).
的取值范围(直接写出结果).
【答案】(1)![]() ;(2)横坐标为
;(2)横坐标为![]() 或
或![]() ;(3)①
;(3)①![]() 的取值范围是
的取值范围是![]() 或
或![]() 或
或![]() ②
②![]()
【解析】
(1)根据一次函数性质及点的坐标利用待定系数法求解析式即可;
(2)根据题意求出图像F的函数关系式,再将纵坐标2代入解析式即可求得对应点横坐标的值;
(3)①利用函数图像特征根据题意画出图形,分类讨论即可;②根据题意运用二次函数图像性质进行分类讨论即可求出t的取值范围.
解:(1)依题意可知,![]() ,
,
则函数![]() 的
的![]() ,且函数过点(
,且函数过点(![]() ,0),
,0),
∴函数![]() 的解析式为
的解析式为![]() ,
,
故答案为:![]() ;
;
(2)解:函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,
时,
图象![]() 的解析式为
的解析式为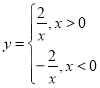 ,
,
把![]() 分别代入,得
分别代入,得![]() 或
或![]() .解得
.解得![]() 或
或![]() .
.
![]() 该点的横坐标为
该点的横坐标为![]() 或
或![]() .
.
(3)①解:图象的解析式为:
把![]() 代入
代入![]() 中,得
中,得![]() .
.
把![]() 代入
代入![]() ,得
,得![]() .
.
把![]() 代入
代入![]() 中,得
中,得![]() .
.
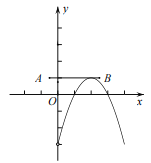
如图,当图象![]() 与线段
与线段![]() 只有一个公共点时,
只有一个公共点时,
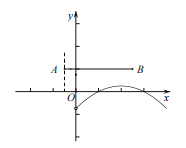
有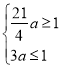 解得:
解得:![]() ;
;
如图,当图象![]() 顶点在线段
顶点在线段![]() 上时,
上时,![]() 与线段
与线段![]() 只有一个公共点时,
只有一个公共点时,
![]() .
.
![]() .
.
如图,当图象![]() 对称轴左侧抛物线与线段
对称轴左侧抛物线与线段![]() 只有一个公共点时
只有一个公共点时
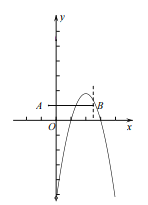
有![]() ,
,
解得![]() ,
,
综上所述,![]() 的取值范围是
的取值范围是![]() 或
或![]() 或
或![]() ;
;
②当![]() 时,函数
时,函数![]() 的解析式为
的解析式为![]() ,
,
则,函数顶点坐标为(2,![]() ),
),
∴函数顶点坐标关于x轴对称点的坐标为(2,2),
当![]() 时,可求得
时,可求得![]() ,
,![]() ,
,
∴当![]() 时,点C在
时,点C在![]() 范围内
范围内![]() 处函数取最大时,为不定值,
处函数取最大时,为不定值,
当![]() 时,且
时,且![]() ,此时点C在
,此时点C在![]() 时函数值最大,为2,
时函数值最大,为2,
∴![]() ,即
,即![]() ,
,
当![]() 时,点C在
时,点C在![]() 时函数值最大,为不定值,
时函数值最大,为不定值,
∴要使得在![]() 时,
时,![]() 的最大值始终保持不变,
的最大值始终保持不变,![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种新型小家电,A型每台进价40元,售价50元,B型每台进价32元,售价40元,4月份售出A型40台,且销售这两种小家电共获利不少于800元.
(1)求4月份售出B型小家电至少多少台?
(2)经市场调查,5月份A型售价每降低1元,销量将增加10台;B型售价每降低1元,销量将在4月份最低销量的基础上增加15台.为尽可能让消费者获得实惠,商场计划5月份A、B两种小家电都降低相同价格,且希望销售这两种小家电共获利965元,则这两种小家电都应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组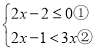
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:

(4)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
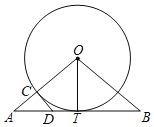
A.DC=DTB.AD=![]() DTC.BD=BOD.2OC=5AC
DTC.BD=BOD.2OC=5AC
查看答案和解析>>
科目:初中数学 来源: 题型:
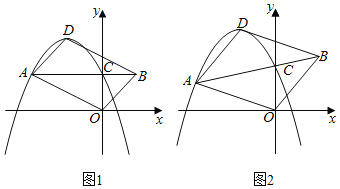
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
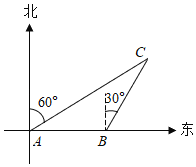
【题目】如图,一艘船由西向东航行,在A处测得北偏东60°方向上有一座灯塔C,再向东续航行60km到达B处,这时测得灯塔C在北偏东30°方向上,已知在灯塔C的周围47km内有暗礁,问这艘船继续向东航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:

(Ⅰ)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为______;
的值为______;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是![]() 上一点,∠ADC=∠G.
上一点,∠ADC=∠G.
(1)求证:∠1=∠2;
(2)点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
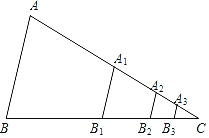
【题目】如图,△ABC的面积为4,分别取AC,BC两边的中点A1,B1,记△A1B1C的面积为S1;再分别取A1C,B1C的中点A2,B2,记△A2B2C的面积为S2,再分别取A2C,B2C的中点A3,B3,记△A3B3C的面积为S3;则S3的值等于_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com