
分析 (1)去括号、移项、合并同类项、系数化为1即可求解;
(2)去分母、去括号、移项、合并同类项、系数化为1即可求解;
(3)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(4)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)去括号,得:3x+4<6+2x-4,
移项得:3x-2x<6-4-4,
合并同类项,得:x<2.
在数轴上表示解集为: ;
;
(2)去分母,得:2(2x-1)≤3x-4,
去括号,得:4x-2≤3x-4,
移项得,4x-3x≤-4+2,
合并同类项,得:x≤-2.
在数轴上表示解集为: ;
;
(3)$\left\{\begin{array}{l}{2x+3>5…①}\\{3x-2≤4…②}\end{array}\right.$,
解①得:x>1,
解②得:x≤2.
在数轴上表示解集为:
不等式组的解集是:1<x≤2;
(4)$\left\{\begin{array}{l}{5x-1>3(x+1)…①}\\{\frac{x-2}{2}≤7-\frac{3x}{2}…②}\end{array}\right.$,
解①得:x>1,
解②得:x≤4.
在数轴上表示解集为:
不等式组的解集是:1<x≤4.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.要注意x是否取得到,若取得到则x在该点是实心的.反之x在该点是空心的.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
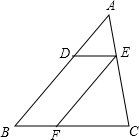 如图,已知DE∥BC,EF平分∠DEC,且∠ADE=50°,∠C=80°.
如图,已知DE∥BC,EF平分∠DEC,且∠ADE=50°,∠C=80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
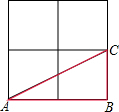 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-3,-3),B(-2,-1),C(-1,-3)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-3)是直角坐标平面上三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com