
【题目】在![]() 中,已知
中,已知![]() ,
,![]() 为
为![]() 的角平分线.\
的角平分线.\
(1)如图1,当![]() 时,在
时,在![]() 边上截取
边上截取![]() ,连接
,连接![]() ,你能发现线段
,你能发现线段![]() 、
、![]() 、
、![]() 之间有怎样的数量关系么?请直接写出你的发现:________________________(不需要证明);
之间有怎样的数量关系么?请直接写出你的发现:________________________(不需要证明);

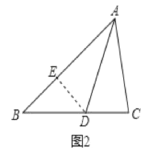
(2)如图2,当![]() 时,线段
时,线段![]() 、
、![]() 、
、![]() 还有(1)中的数量关系么?请证明你的猜想;
还有(1)中的数量关系么?请证明你的猜想;
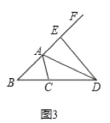
(3)如图3,当![]() 为
为![]() 的外角平分线时,线段
的外角平分线时,线段![]() 、
、![]() 、
、![]() 又有怎样的数量关系?不需要证明,请直接写出你的猜想:______________________.
又有怎样的数量关系?不需要证明,请直接写出你的猜想:______________________.
【答案】(1)AB=AC+CD,理由见解析;(2)还成立,理由见解析;(3)AB+AC=CD,理由见解析;
【解析】
(1)由AD为∠BAC的角平分线,得到∠EAD=∠CAD,通过△AED≌△ACD,得到ED=CD,∠AED=∠ACD=90°,由于∠ACB=90°,∠ACB=2∠B,得到∠B=45°,∠BDE=45°,∠B=∠BDE,根据等腰三角形的性质得到EB=ED,于是得到结论;
(2)如图2,在AB上截取AE=AC,连接ED,由AD为∠BAC的角平分线时,得到∠BAD=∠CAD,通过△AED≌△ACD得到∠AED=∠C,ED=CD,由已知得到∠B=∠EDB,根据等腰三角形的性质得到EB=ED,即可得解;
(3)如图3,在BA的延长线上截取AE=AC,连接ED,由AD为∠BAC的角平分线时,得到∠BAD=∠CAD,通过△AED≌△ACD得到∠AED=∠C,ED=CD,由已知得到∠B=∠EDB,根据等腰三角形的性质得到EB=ED,即可得解.
证明:(1)AB=AC+CD
理由如下:
∵AD为∠BAC的角平分线

∴∠EAD=∠CAD,
在△AED与△ACD中,
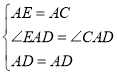
∴△AED≌△ACD(SAS),
∴ED=CD,∠AED=∠ACD=90°,
又∵∠ACB=90°,∠ACB=2∠B,
∴∠B=45°,
∴∠BDE=45°,
∴∠B=∠BDE,
∴EB=ED,
∴EB=CD,
∴AB=AE+EB=AC+CD;
故答案为:AB=AC+CD
(2)结论:还成立.
理由:如图2,在AB上截取AE=AC,连接ED,
∵AD为∠BAC的角平分线时,
∴∠BAD=∠CAD,
在△AED与△ACD中,
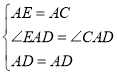
∴△AED≌△ACD(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+EB=AC+CD;
(3)猜想:AB+AC=CD.
证明:如图3,在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,
∴∠EAD=∠CAD,
在△AED与△ACD中,
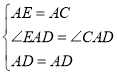
∴△AED≌△ACD(SAS),
∴ED=CD,∠AED=∠ACD,
∴∠FED=∠ACB,
又∵∠ACB=2∠B,
∴∠FED=2∠B,
又∵∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴EB=ED,
∴EA+AB=EB=ED=CD,
∴AC+AB=CD.


科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒.
(1)当t=2时,点P对应的有理数xP=______,PQ=______;
(2)当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;
(3)我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2100元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 点的对应数为
点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若数轴上表示![]() 的点在
的点在![]() 与
与![]() 之间,则
之间,则![]() 的值为_________;
的值为_________;
(4)当![]() 满足_________时,则
满足_________时,则![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,并完成填空:在图1至图3中,己知![]() 的面积为
的面积为![]() .
.
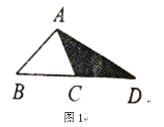
(1)如图1,延长![]() C的边
C的边![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() .若
.若![]() 的面积为
的面积为![]() ,则
,则![]() __________(用含
__________(用含![]() 的代数式表示);
的代数式表示);
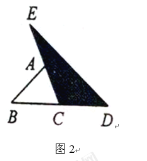
(2)如图2,延长![]() 的边
的边![]() 到点
到点![]() ,延长边
,延长边![]() 到点
到点![]() ,使
,使![]() ,
,![]() ,连结
,连结![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() __________(用含
__________(用含![]() 的代数式表示);
的代数式表示);
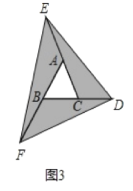
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,得到△DEF(如图3),若阴影部分的面积为S3,则S3=___(用含a的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城间的铁路路程为1600千米,经过技术改造,列车实施了提速,提速后比提速前速度增加了20千米/小时,列车从甲城到乙城行驶时间减少4小时,这条铁路在现有条件下安全行驶速度不得超过140千米/小时,请你用学过的知识说明在这条铁路的现有条件下列车是否还可以再提速。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com