
����Ŀ��ij��˾��A��B�����ͺŵĿͳ���15�������ǵ��ؿ�����ÿ������ͳ��������±���ʾ����֪��15���ͳ�������������£����ؿ�570��
A�ͺſͳ� | B�ͺſͳ� | |
�ؿ�������/���� | 45 | 30 |
���Ԫ/���� | 400 | 280 |
������������ | a | b |
��1�������a��b��ֵ��
��2��ij��ѧ�ƻ�����A��B�����ͺŵĿͳ���5����ͬʱ�����꼶ʦ�������زμ����ʵ�������֪����ѧ����ܷ��ò�����1900Ԫ�� ������������ö�����A�ͺſͳ���
�������꼶��ʦ������195�ˣ���д�����п��ܵ����������ȷ����ʡǮ���������
���𰸡�
��1���⣺������� ![]() �����
����� ![]()
��2���⣺����ƻ�����A���ͺŵĿͳ�x������ƻ�����B���ͺŵĿͳ���5��x������
���������400x+280��5��x����1900�����x��4 ![]() ��
��
��Ϊxȡ�Ǹ�������
����x�����ֵΪ4��
�����������4��A�ͺſͳ���
�ڸ��������45x+30��5��x����195�����x��3��
��x��4 ![]() ��
��
����3��x��4 ![]() ��
��
��ΪxΪ��������
����x=3��4��
���п��ܵ������Ϊ
����һ������A���ͺŵĿͳ�3��������B���ͺŵĿͳ�2������ʱ����Ϊ3��400+2��280=1760��Ԫ��
������������A���ͺŵĿͳ�4��������B���ͺŵĿͳ�1������ʱ����Ϊ4��400+1��280=1880��Ԫ��
������ʡǮ�������Ϊ����A���ͺŵĿͳ�3��������B���ͺŵĿͳ�2��
����������1�����ÿͳ�������Ϊ15����15���ͳ�������������£����ؿ�570�˿��з����飬Ȼ��ⷽ�̼��ɵõ�a��b��ֵ����2������ƻ�����A���ͺŵĿͳ�x������ƻ�����B���ͺŵĿͳ���5��x���������ø���ѧ����ܷ��ò�����1900Ԫ���в���ʽ400x+280��5��x����1900��Ȼ��ⲻ��ʽ������xΪ������������˽⼯���������������ɣ� ���������ֿͳ�������������195�в���ʽ�õ�+30��5��x����195�����x��3������x��4 ![]() �����ǵõ�x=3��4��Ȼ��д������������ͨ�������������ķ��õõ���ʡǮ�������
�����ǵõ�x=3��4��Ȼ��д������������ͨ�������������ķ��õõ���ʡǮ�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ� ��
A.��ͬһƽ���ڣ���ֱ����һ�㣬��������ֱ������ֱ֪�ߴ�ֱ
B.��ƽ�Ƶõ�������ͼ�εĸ����Ӧ�������ഹֱ
C.���⡰һ���ǵ����һ������ǡ���������
D.![]() ��������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�����B=60�㣬��E��F�ֱ���AB��AD�ϣ���BE=AF�����AEC+��AFC�Ķ������ڣ�������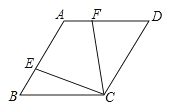
A.120��
B.140��
C.160��
D.180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����һ��������ֽ����һ����Ϊ4cm�ij������ٴ�ʣ�µij�����ֽƬ�ϼ�ȥһ����Ϊ5cm�ij�����������μ��µij������������ȣ���ôÿһ���������Ϊ�� �� 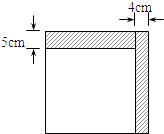
A.16cm2
B.20cm2
C.80cm2
D.160cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽�����꼶1000��ѧ�������彡��������Ӹ��꼶�����ȡ��������ѧ���������ǰ����أ���Ϊ��������λ��kg���ֳ����飨A��39.5��46.5��B��46.5��53.5��C��53.5��60.5��D��60.5��67.5��E��67.5��74.5����������ͳ�����ݻ��������������в�������ͳ��ͼ��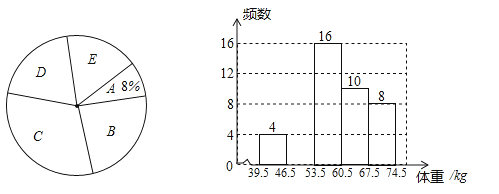
����������⣺
��1����γ������������������ ����ȫƵ���ֲ�ֱ��ͼ��
��2��C��ѧ����Ƶ��Ϊ ��������ͳ��ͼ��D���Բ�Ľ��� �ȣ�
��3��������Ƹ�У�����꼶���س���60kg��ѧ����Լ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������������ƽ���ı��ε��ǣ�������
A. ����Աߵij��ֱ���3��5
B. �������ߵij��ֱ���3��5����һ���Խ��߳�Ϊ9
C. һ�ߵij�Ϊ7�������Խ��ߵij��ֱ�Ϊ6��8
D. һ�ߵij�Ϊ7�������Խ��ߵij��ֱ�Ϊ6��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=��![]() �� ����
�� ����
������ͼ����һ�������ޣ�
�ڵ㣨��2��4��������ͼ���ϣ�
�۵�l��x��2ʱ��y��ȡֵ��Χ�ǩ�8��y����4��
�����ú�����ͼ������������A ��x1 �� y1����B��x2 �� y2������ô��x1��x2ʱ��y1��y2
����������ȷ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com