
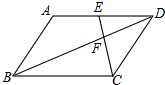
 如图,在?ABCD中,点E是AD的中点,连接CE、BD交于点F,BD=12,则DF=4.
如图,在?ABCD中,点E是AD的中点,连接CE、BD交于点F,BD=12,则DF=4. 分析 先利用平行四边形的性质得AD=BC,AD∥BC,则DE=$\frac{1}{2}$BC,再利用DE∥BC可判断△DEF∽△BCF,则利用相似比可得BF=2DF,然后利用BD=DF+BF=12可计算出DF.
解答 解:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
而点E是AD的中点,
∴DE=$\frac{1}{2}$BC,
∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{1}{2}$,
∴BF=2DF,
∵BD=DF+BF=12,
∴DF+2DF=12,
∴DF=4.
故答案为4.
点评 本题考查相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时主要利用相似比进行几何计算.也考查了平行四边形的性质.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x(a-b)=ax-bx | B. | $\frac{1}{{x}^{2}}$-1=($\frac{1}{x}$+1)($\frac{1}{x}$-1) | ||
| C. | x2-1=(x+1)(x-1) | D. | x2-1+y2=(x-1)(x+1)+y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②⑥ | B. | ①②⑥ | C. | ④⑤⑥ | D. | ①⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-$\frac{1}{4}$ | B. | m≥-$\frac{1}{4}$ | C. | m>-$\frac{1}{4}$且m≠0 | D. | m≥-$\frac{1}{4}$且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm、3cm、5cm、7cm | B. | 1cm、2cm、3cm、4cm | ||
| C. | 25cm、35cm、45cm、55cm | D. | 1cm、2cm、20cm、40cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com