
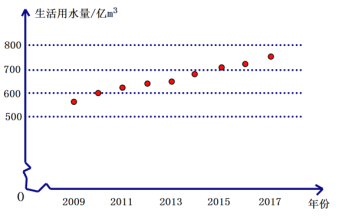
ЁОЬтФПЁПЮвЙњУПФъЕФзмгУЫЎжївЊАќРЈЫФДѓЗНУцЃКХЉвЕгУЫЎЁЂЙЄвЕгУЫЎЁЂЩњЛюгУЫЎЁЂЦфЫћгУЫЎ. 2017ФъЃЌЮвЙњХЉвЕгУЫЎСПдМ![]() вк
вк![]() ЃЈеМзмгУЫЎСПЕФ
ЃЈеМзмгУЫЎСПЕФ![]() ЃЉЃЌЙЄвЕгУЫЎСПдМЮЊ
ЃЉЃЌЙЄвЕгУЫЎСПдМЮЊ![]() вк
вк![]() ЃЌЩњЛюгУЫЎСПОпЬхМћЯТБэ.
ЃЌЩњЛюгУЫЎСПОпЬхМћЯТБэ.
2019-2017ФъШЋЙњЩњЛюгУЫЎСПБэЃЈЕЅЮЛЃКвк![]() ЃЉ
ЃЉ
ФъЗн | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
гУЫЎСП |
|
|
|
|
|
|
|
|
|
ЃЈ1ЃЉ2017ФъШЋЙњзмгУЫЎСПдМЮЊ вк![]() ЃЌЦфЫћгУЫЎдМЮЊ вк
ЃЌЦфЫћгУЫЎдМЮЊ вк![]() .
.
ЃЈ2ЃЉИљОнЁА2019-2017ФъШЋЙњЩњЛюгУЫЎСПБэЁБЃЌдкЦНУцжБНЧзјБъЯЕжаУшГіБэжаИїЖдЪ§жЕЫљЖдгІЕФЕуЃЈЦфжаКсзјБъБэЪОФъЗнЃЌзнзјБъБэЪОгУЫЎСПЃЉПЩЗЂЯжЃЌетаЉЕуНќЫЦЕФТфдкФГЬѕжБЯпЩЯ.
ЂйгУППНќОЁПЩФмЖрЕуЕФжБЯпРДБэЪОгУЫЎСПЕФетжжЧїЪЦЃЌЧыдкЩЯЭМжаЛГіетЬѕжБЯпЃЛ
ЂкИљОнЫљЛЕФжБЯпЃЌЙРМЦ2018ФъШЋЙњЩњЛюгУЫЎСПЃЌВЂЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ,
,![]() ЃЛЃЈ2ЃЉЂйМћЯъНтЃЛЂкЙРМЦ2018ФъЕФШЋЙњЩњЛюгУЫЎСПдМЮЊ
ЃЛЃЈ2ЃЉЂйМћЯъНтЃЛЂкЙРМЦ2018ФъЕФШЋЙњЩњЛюгУЫЎСПдМЮЊ![]() вк
вк![]() ЃЌРэгЩМћЯъНт
ЃЌРэгЩМћЯъНт
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХЉвЕгУЫЎСПдМ![]() вк
вк![]() ЃЈеМзмгУЫЎСПЕФ
ЃЈеМзмгУЫЎСПЕФ![]() ЃЉЧѓГізмгУЫЎСПЃЌдйЧѓЦфЫќгУЫЎСПМДПЩЃЛ
ЃЉЧѓГізмгУЫЎСПЃЌдйЧѓЦфЫќгУЫЎСПМДПЩЃЛ
ЃЈ2ЃЉЂйИљОнвЊЧѓЛЭММДПЩЃЛЂкИљОнЫљЛЕФжБЯпЃЌЙРМЦ2018ФъШЋЙњЩњЛюгУЫЎСПМДПЩЃЌД№АИВЛЮЈвЛ.
Нт:(1)3660ЁТ![]() =
=![]() ,
,
6100-3660-1401-750=![]()
ЙЪД№АИЮЊ![]() ,
,![]() .
.
(2) ЂйШчЭМЃЌЛЭМ:
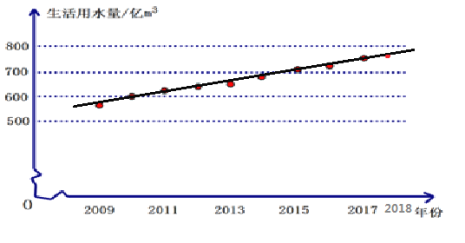
ЂкД№АИВЛЮЈвЛЃЌ Шч:ЙРМЦ2018ФъЕФШЋЙњЩњЛюгУЫЎСПдМЮЊ![]() вк
вк![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН2x+6НЛxжсгкAЃЌНЛyжсгкBЃЎ

ЃЈ1ЃЉжБНгаДГіAЃЈЁЁ ЁЁЃЌЁЁ ЁЁЃЉЃЌBЃЈЁЁ ЁЁЃЌЁЁ ЁЁЃЉЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуEЮЊжБЯпyЃНx+2ЩЯвЛЕуЃЌЕуFЮЊжБЯпyЃН![]() xЩЯвЛЕуЃЌШєвдAЃЌBЃЌEЃЌFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓЕуEЃЌFЕФзјБъ
xЩЯвЛЕуЃЌШєвдAЃЌBЃЌEЃЌFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓЕуEЃЌFЕФзјБъ
ЃЈ3ЃЉШчЭМ2ЃЌЕуCЃЈmЃЌnЃЉЮЊЯпЖЮABЩЯвЛЖЏЕуЃЌDЃЈЉ7mЃЌ0ЃЉдкxжсЩЯЃЌСЌНгCDЃЌЕуMЮЊCDЕФжаЕуЃЌЧѓЕуMЕФзнзјБъyКЭКсзјБъxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГідкЕуCвЦЖЏЙ§ГЬжаЕуMЕФдЫЖЏТЗОЖГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
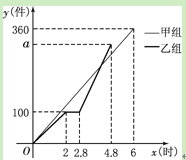
ЁОЬтФПЁПМзЁЂввСНзщЙЄШЫЭЌЪБМгЙЄФГжжСуМўЃЌввзщЙЄзїжагавЛДЮЭЃВњИќЛЛЩшБИЃЌИќЛЛЩшБИ
КѓЃЌввзщЕФЙЄзїаЇТЪЪЧдРДЕФ2БЖЃЎСНзщИїздМгЙЄСуМўЕФЪ§СП![]() (Мў)гыЪБМф
(Мў)гыЪБМф![]() (ЪБ)ЕФКЏЪ§ЭМ
(ЪБ)ЕФКЏЪ§ЭМ
ЯѓШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓМззщМгЙЄСуМўЕФЪ§СПyгыЪБМф![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎЃЈ2ЗжЃЉ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎЃЈ2ЗжЃЉ
ЃЈ2ЃЉЧѓввзщМгЙЄСуМўзмСП![]() ЕФжЕЃЎЃЈ3ЗжЃЉ
ЕФжЕЃЎЃЈ3ЗжЃЉ
ЃЈ3ЃЉМзЁЂввСНзщМгЙЄГіЕФСуМўКЯдквЛЦ№зАЯфЃЌУПЙЛ300МўзАвЛЯфЃЌСуМўзАЯфЕФЪБМфКіТдВЛМЦЃЌЧѓОЙ§ЖрГЄЪБМфЧЁКУзАТњЕк1ЯфЃПдйОЙ§ЖрГЄЪБМфЧЁКУзАТњЕк2ЯфЃПЃЈ5ЗжЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпyЃНkx+kЉ2ОЙ§ЕуЃЈmЃЌn+1ЃЉКЭЃЈm+1ЃЌ2n+3ЃЉЃЌЧвЉ2ЃМkЃМ0ЃЌдђnЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. Љ2ЃМnЃМ0B. Љ4ЃМnЃМЉ2C. Љ4ЃМnЃМ0D. 0ЃМnЃМЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
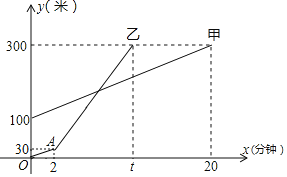
ЁОЬтФПЁПМзЁЂввСНШЫЯрдМжмФЉбиЭЌвЛЬѕТЗЯпЕЧЩНЃЌМзЁЂввСНШЫОрЕиУцЕФИпЖШyЃЈУзЃЉгыЕЧЩНЪБМфxЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌИљОнЭМЯѓЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬт
ЃЈ1ЃЉМзЕЧЩНЕФЫйЖШЪЧУПЗжжгЁЁ УзЃЛввдкAЕиЬсЫйЪБЃЌМзОрЕиУцЕФИпЖШЮЊЁЁ УзЃЛ
ЃЈ2ЃЉШєввЬсЫйКѓЃЌввЕФЫйЖШЪЧМзЕЧЩНЫйЖШЕФ3БЖЃЛ
ЂйЧѓввЕЧЩНШЋЙ§ГЬжаЃЌЕЧЩНЪБОрЕиУцЕФИпЖШyЃЈУзЃЉгыЕЧЩНЪБМфxЃЈЗжжгЃЉжЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЂкввМЦЛЎдкЫћЬсЫйКѓ5ЗжжгФкзЗЩЯМзЃЌЧыХаЖЯввЕФМЦЛЎФмЪЕЯжТ№ЃПВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБxЮЊЖрЩйЪБЃЌМзЁЂввСНШЫОрЕиУцЕФИпЖШВюЮЊ80УзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуEЃЌFдкОиаЮЕФБпADЃЌBCЩЯЃЌЕуBгыЕуDЙигкжБЯпEFЖдГЦЃЎЩшЕуAЙигкжБЯпEFЕФЖдГЦЕуЮЊGЃЎ
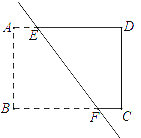
ЃЈ1ЃЉЛГіЫФБпаЮABFEЙигкжБЯпEFЖдГЦЕФЭМаЮЃЛ
ЃЈ2ЃЉШєЁЯFDCЃН16ЁуЃЌжБНгаДГіЁЯGEFЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉШєBCЃН4ЃЌCDЃН3ЃЌаДГіЧѓЯпЖЮEFГЄЕФЫМТЗЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН4ЃЌADЃН5ЃЌADЁЂABЁЂBCЗжБ№гыЁбOЯрЧагкEЁЂFЁЂGШ§ЕуЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛBCгкЕуMЃЌдђDMЕФГЄЮЊ(ЁЁЁЁ)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
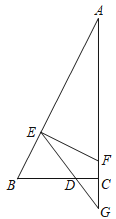
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЁїABCжаЃЌЁЯACB=90ЁуЃЌBC=2ЃЌAC=4ЃЌЕуDдкЩфЯпBCЩЯЃЌвдЕуDЮЊдВаФЃЌBDЮЊАыОЖЛЛЁНЛБпABгкЕуEЃЌЙ§ЕуEзїEFЁЭABНЛБпACгкЕуFЃЌЩфЯпEDНЛЩфЯпACгкЕуGЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїEFGЁзЁїAEGЃЛ
ЃЈ2ЃЉЧыЬНОПЯпЖЮAFгыFGЕФБЖЪ§ЙиЯЕЃЌВЂжЄУїФуЕФНсТлЁЃ
ЃЈ3ЃЉЩшFG=xЃЌЁїEFGЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂжБНгаДГіxЕФШЁжЕЗЖЮЇЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЙКНјФГжжПѓЪЏдСЯ300ЖжЃЌгУгкЩњВњМзЁЂввСНжжВњЦЗЃЌЩњВњ1ЖжМзВњЦЗЛђ1ЖжввВњЦЗЫљашИУПѓЪЏКЭУКдСЯЕФЖжЪ§ШчЯТБэ:
ВњЦЗзЪдД | Мз | вв |
ПѓЪЏЃЈЖжЃЉ | 10 | 4 |
УКЃЈЖжЃЉ | 4 | 8 |
ЩњВњ1ЖжМзВњЦЗЫљашГЩБОЗбгУЮЊ4000дЊЃЌУПЖжЪлМл4600дЊЃЛ
ЩњВњ1ЖжввВњЦЗЫљашГЩБОЗбгУЮЊ4500дЊЃЌУПЖжЪлМл5500дЊЃЌ
ЯжНЋИУПѓЪЏдСЯШЋВПгУЭъЃЌЩшЩњВњМзВњЦЗxЖжЃЌввВњЦЗmЖжЃЌЙЋЫОЛёЕУЕФзмРћШѓЮЊyдЊ.
ЃЈ1ЃЉаДГіmгыxжЎМфЕФЙиЯЕЪН
ЃЈ2ЃЉаДГіyгыxжЎМфЕФКЏЪ§БэДяЪНЃЌВЂаДГіздБфСПЕФЗЖЮЇ
ЃЈ3ЃЉШєгУУКВЛГЌЙ§200ЖжЃЌЩњВњМзВњЦЗЖрЩйЖжЪБЃЌЙЋЫОЛёЕУЕФзмРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com