
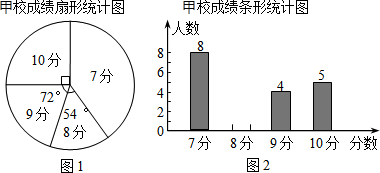
 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数 | 11 | 0 | 8 |
分析 (1)直接根据扇形统计图的已知条件求解即可求得答案;
(2)首先求得总人数,继而可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两名男同学恰好在同一组的情况,再利用概率公式求解即可求得答案.
解答 解:(1)由扇形统计图可得:”7分”所在扇形的圆心角为:360°-90°-72°-54°=144°.
故答案为:144;
(2)∵10分的5人,占$\frac{90}{360}$×100%=25%,
∴每个学校派出的人数为:5÷25%=20(人),
∴甲校8分的人数为:20-8-4-5=3(人),
乙校9分的人数为:20-11-0-8=1(人);
∴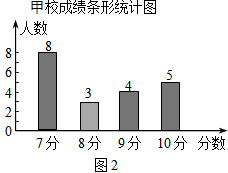
| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数 | 11 | 0 | 1 | 8 |
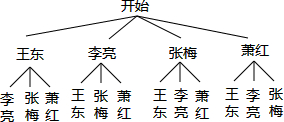
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.注意掌握圆心角与百分比之间的关系.用到的知识点为:概率=所求情况数与总情况数之比.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
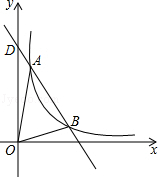 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点,与两坐标轴的交点分别为C、D.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点,与两坐标轴的交点分别为C、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
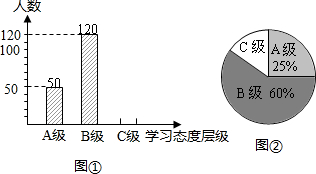 某地教育部门对九年级学生的“学习态度”进行了一次抽样调查,把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣,要求被调查的学生从A、B、C三项中必选且只能选择一项,结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
某地教育部门对九年级学生的“学习态度”进行了一次抽样调查,把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣,要求被调查的学生从A、B、C三项中必选且只能选择一项,结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
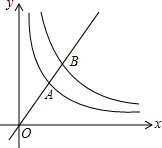 如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.
如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com