
����Ŀ��ij���������һ��ɱ�Ϊ20Ԫ/���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
���۵���x��Ԫ�M���� | �� | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | �� |
��1���о����֣�ÿ��������y�뵥��x����һ�κ�����ϵ�����y��x�Ĺ�ϵʽ��
��2��������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���45Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��
���𰸡�(1)y����10x+800��(2)���۵��۶�Ϊ40Ԫ/��ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��
��������
��1�����ô���ϵ�������ɵã�
��2��������������=�������������������ɵù���x��һԪ���η��̣���֮���ɵã�
(1)��y��kx+b��
��������ɵ�![]() ��
��
��ã�![]() ��
��
��y����10x+800��
(2)�������⣬�ã���x��20������10x+800����8000��
�������ã�x2��100x+2400��0��
��ã�x1��40��x2��60��
�����۵�����߲��ܳ���45Ԫ/����
��x��40��
�����۵��۶�Ϊ40Ԫ/��ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1cm��3cm��5cm��7cm��9cm�������߶��У���ѡ�������Թ��������εĸ�����________%��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AC��BD�ཻ�ڵ�O��O��AC���е㣬AB//DC��AC=10��BD=8.
��1����֤���ı���ABCD��ƽ���ı��Σ�
��2����AC��BD����ƽ���ı���ABCD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ1��ͼ2�ֱ���![]() �����������е�ÿ��С�����εı߳���Ϊ1���밴����Ҫ��ֱ���Ӧ��ͼ�Σ�������ͼ�ε�ÿ�������������С�����εĶ����ϣ�
�����������е�ÿ��С�����εı߳���Ϊ1���밴����Ҫ��ֱ���Ӧ��ͼ�Σ�������ͼ�ε�ÿ�������������С�����εĶ����ϣ�

(1)��ͼ1�л���һ���ܳ�Ϊ![]() ������
������![]() (��������)��
(��������)��
(2)��ͼ2�л���һ�����Ϊ9��ƽ���ı���![]() ��������
��������![]() ����ֱ��д��ƽ���ı���
����ֱ��д��ƽ���ı���![]() ���ܳ���
���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���![]() �У�
�У�![]() ������Ϊ��
��������![]() ��
��![]() ��
��
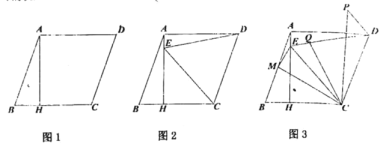
(1)��ͼ1����֤��![]() ��
��
(2)��ͼ2����![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ����֤��
����֤��![]() ��
��
(3)��(2)�������£���ͼ3����![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬�ֱ�����
���е㣬�ֱ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
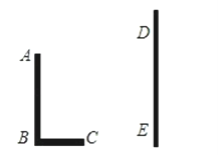
����Ŀ����֪����ͼ��AB��DE��ֱ���ڵ����ϵ�����������AB=7m��ijһʱ��AB��̫�����µ�ͶӰBC=4m��
��1��������ͼ�л�����ʱDE�������µ�ͶӰ��
��2���ڲ���AB��ͶӰʱ��ͬʱ������DE�������µ�ͶӰ��Ϊ8m������DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
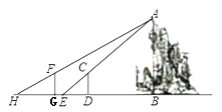
����Ŀ����ɽ���ж����쾰���ܣ��뽨����ֲ�����ϳɸ��ڱ仯�ľ��£�ij����һ����ɽ��С����С�۵�ͬѧ����һЩ�������ߺ���ѧ�ļ���֪ʶ����������ɽ�ĸ߶��������Լ�����֪ʶ������֪ʶ����������ͼ���������£�С��վ��ˮƽ�����D������ʱС�����ߵ�Ӱ�Ӷ������ɽ��Ӱ�Ӷ���E�غϣ���ʱС������CD��Ӱ��DE=2�ף�һ��ʱ���С����D����BD�ķ�������3.6����G������ʱС�����ߵ�Ӱ�Ӷ������ɽ��Ӱ�Ӷ���H�غϣ���ʱС�����ߵ�Ӱ��GH=2.4�ף���֪С��������CD=FG=1.5�ף���G��E��D����ֱ��BH�ϣ�AB��BH��CD��BH��GF��BH��������������ṩ�������Ϣ�������ɽ�ĸ߶�AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
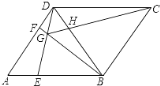
����Ŀ����ͼ��������ABCD�У�tanA= ![]() ����E��F�ֱ���AB��AD������ĵ㣨����˵��غϣ�����AE=DF������BF��DE�ཻ�ڵ�G������CG��BD�ཻ�ڵ�H���������¼������ۣ���1����AED�ա�DFB����2��CG��BDһ������ֱ����3����BGE�Ĵ�СΪ��ֵ����4��S�ı���BCDG=
����E��F�ֱ���AB��AD������ĵ㣨����˵��غϣ�����AE=DF������BF��DE�ཻ�ڵ�G������CG��BD�ཻ�ڵ�H���������¼������ۣ���1����AED�ա�DFB����2��CG��BDһ������ֱ����3����BGE�Ĵ�СΪ��ֵ����4��S�ı���BCDG= ![]() CG2��������ȷ���۵����Ϊ________��
CG2��������ȷ���۵����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2016��Ϊ���á�����ƶ����Ͷ���ʽ�1200��Ԫ������ذ��ã����滮Ͷ����ذ����ʽ����ƽ���������������ڱ��ֲ��䣬��֪2018����2016��Ļ�����������Ͷ����ذ����ʽ�1500��Ԫ��
��1��2017��õ�Ͷ����ذ����ʽ�Ϊ����Ԫ��
��2����2017����ذ��õľ���ʵʩ�У��õ�Ҫ��Ͷ���������Ȱ�Ǩ�ⷿ�������ʽ���2017��õ�Ͷ����ذ����ʽ��25%���涨ǰ1000��������1000������ÿ��ÿ�콱��8Ԫ��1000���Ժ�ÿ��ÿ�콱��5Ԫ�����ⷿ400����㣬��2017��õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com