
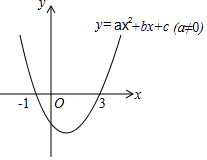 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用抛物线与x轴的交点可抛物线的对称性得到抛物线的对称轴为直线x=1,则根据抛物线的对称轴方程得到b=-2a,则可对①进行判断;利用函数图象得到当-1≤x≤3时,函数图象都不在x轴上方,则y≤0,则可②进行判断;利用抛物线开口方向得到a>0,利用对称性方程得到b<0,利用抛物线与y轴的交点位置得到c<0,则可对③进行判断;利用x=3时,y=0;x=2时,y<0,可对④进行判断;利用抛物线的顶点在第四象限和抛物线的顶点坐标公式可对⑤进行判断;利用二次函数的性质可对⑥直接判断.
解答 解:∵抛物线与x轴的交点为(-1,0),(3,0),
∴抛物线的对称轴为直线x=1,
∴-$\frac{b}{2a}$=1,即b=-2a,所以①正确;
当-1≤x≤3时,函数图象都不在x轴上方,则y≤0,所以②错误;
∵抛物线开口向下,
∴a>0,
∴b=-2a<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以③错误;
∵x=3时,y=0;x=2时,y<0,
∴9a+3b+c=0,4+2b+c<0,所以④正确;
∵抛物线的顶点在第四象限,
∴$\frac{4ac-{b}^{2}}{4a}$<0,所以⑤正确
∵抛物线的对称轴为直线x=1,
∴(1,y2)是抛物线的顶点,
∴y1>y2.所以⑥正确.
故选C.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的图象于系数的关系.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
 一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)
一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)| 滑行时间t/s | 0 | 1 | 2 | 3 | 4 |
| 滑行距离s/m | 0 | 4.5 | 14 | 28.5 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
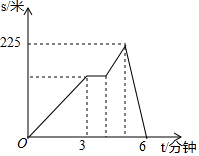 小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.
小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com