
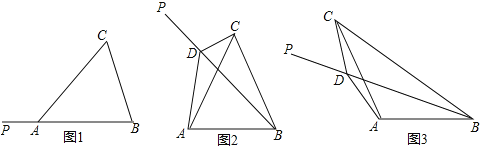
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
【答案】(1)=,BD=CD+AD;(2)证明见试题解析;(3)BD+CD=![]() AD.
AD.
【解析】
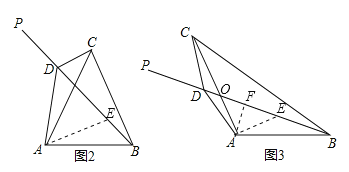
试题分析:(1)如图2,由∠CDP=120°,得出∠CDB=60°,则∠CDB=∠BAC=60°,所以A、B、C、D四点共圆,由圆周角定理得出∠ACD=∠ABD;在BP上截取BE=CD,连接AE.利用SAS证明△DCA≌△EBA,得到AD=AE,∠DAC=∠EAB,再证明△ADE是等边三角形,得到DE=AD,进而得出BD=CD+AD.
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.先证△DOC∽△AOB,得到∠DCA=∠EBA.再利用SAS证明△DCA≌△EBA,得到AD=AE,∠DAC=∠EAB.由∠CAB=∠CAE+∠EAB=120°,得出∠DAE=120°,由等腰三角形的性质及三角形内角和定理求出∠ADE=∠AED=30°.解Rt△ADF,得出DF=![]() AD,那么DE=2DF=
AD,那么DE=2DF=![]() AD,进而得出BD=DE+BE=
AD,进而得出BD=DE+BE=![]() AD+CD,即BD﹣CD=
AD+CD,即BD﹣CD=![]() AD;
AD;
(3)同(2)证明可以得出BD+CD=![]() AD.
AD.
试题解析:(1)如图2,∵∠CDP=120°,∴∠CDB=60°,∵∠BAC=60°,∴∠CDB=∠BAC=60°,∴A、B、C、D四点共圆,∴∠ACD=∠ABD.在BP上截取BE=CD,连接AE.在△DCA与△EBA中,∵AC=AB,∠ACD=∠ABE,CD=BE,∴△DCA≌△EBA(SAS),∴AD=AE,∠DAC=∠EAB,∵∠CAB=∠CAE+∠EAB=60°,∴∠DAE=60°,∴△ADE是等边三角形,∴DE=AD.∵BD=BE+DE,∴BD=CD+AD.故答案为:=,BD=CD+AD;
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.
∵∠CDP=60°,∴∠CDB=120°.∵∠CAB=120°,∴∠CDB=∠CAB,∵∠DOC=∠AOB,∴△DOC∽△AOB,∴∠DCA=∠EBA.在△DCA与△EBA中,∵AC=AB,∠ACD=∠ABE,CD=BE,∴△DCA≌△EBA(SAS),∴AD=AE,∠DAC=∠EAB.∵∠CAB=∠CAE+∠EAB=120°,∴∠DAE=120°,∴∠ADE=∠AED=(180°-120°)÷2=30°.∵在Rt△ADF中,∠ADF=30°,∴DF=![]() AD,∴DE=2DF=
AD,∴DE=2DF=![]() AD,∴BD=DE+BE=
AD,∴BD=DE+BE=![]() AD+CD,∴BD﹣CD=
AD+CD,∴BD﹣CD=![]() AD;
AD;
(3)BD+CD=![]() AD.
AD.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若A(x1,y1)、B(x2,y2)是一次函数y=ax―3x+5图像上的不同的两个点,记W=(x1―x2)( y1―y2),则当W<0时,a的取值范围是 ( )
A. a<0 B. a>0 C. a<3 D. a>3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
B.“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件
C.“同位角相等”这一事件是不可能事件
D.“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举办一年一届的科技文化艺术节活动,需制作一块活动展板,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
(1)两个人合作需要天完成;
(2)现由徒弟先做1天,再两个合作,问:还需几天可以完成这项工作?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与x之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的底边BC=8cm,腰长AB=5cm,一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动,当点P运动到PA与腰垂直的位置时,点P运动的时间应为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;
(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,
(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com