
如图,已知:AB,CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE,QF,试探讨QE,QF的大小关系,并说明理由
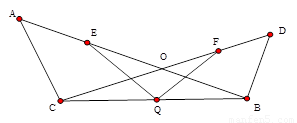
QE=QF,证明见解析.
【解析】
试题分析:直观上看两条线段相等,线段相等一般用三角形的全等证明,但是本题中无法找到全等的三角形,所以选择其他方法,里面有等腰三角形,又有底边上的中点,考虑作中线,于是可以得到直角三角形,而线段BC是两个直角三角形的公共斜边,从而找到两条线段之间的关系,由题,如图, 连接EC,FA,∵AC=CO,E为AO的中点,∴CE⊥AB,∴∠BEC=90°,在Rt△BEC中,EQ=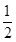 BC,同理可证FQ=
BC,同理可证FQ=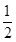 BC,∴QE=QF.
BC,∴QE=QF.
试题解析:如图,连接EC,FA,
∵AC=CO,E为AO的中点,
∴CE⊥AB,
∴∠BEC=90°,
在Rt△BEC中,EQ=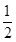 BC,
BC,
同理可证FQ=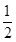 BC,
BC,
∴QE=QF.
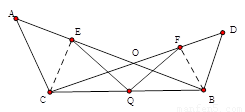
考点:斜边上的中线等于斜边的一半.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
 (2013•温州一模)如图,已知线段AB,
(2013•温州一模)如图,已知线段AB,查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.
如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com