
【题目】如图,扇形OAB的圆心角为90°,点C、D是![]() 的三等分点,半径OC、OD分别与弦AB交于点E、F,下列说法错误的是( )
的三等分点,半径OC、OD分别与弦AB交于点E、F,下列说法错误的是( )
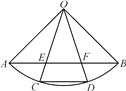
A.AE=EF=FBB.AC=CD=DB
C.EC=FDD.∠DFB=75°
【答案】A
【解析】
试题利用点C,D是![]() 的三等分点,得出AC=CD=DB,∠AOC=∠COD=∠BOD=
的三等分点,得出AC=CD=DB,∠AOC=∠COD=∠BOD=![]() ∠AOB=30°,再求出∠OBA的度数,利用外角求出∠BFD的度数,通过证△AOE≌△BOF,得出OE=OF,则EC=FD.连接AC,在△ACE中,求证AE=AC,则可证CD=AE=BF,再根据CD>EF得AE、EF、FB 关系.
∠AOB=30°,再求出∠OBA的度数,利用外角求出∠BFD的度数,通过证△AOE≌△BOF,得出OE=OF,则EC=FD.连接AC,在△ACE中,求证AE=AC,则可证CD=AE=BF,再根据CD>EF得AE、EF、FB 关系.
解:∵点C,D是![]() 的三等分点,
的三等分点,
∴AC=CD=DB,∠AOC=∠COD=∠BOD=![]() ∠AOB=30°,
∠AOB=30°,
∴选项B正确;
∵OA=OB,∠AOB=90°,∴∠OAB=∠OBA=45°,
∴∠AEC=∠OAB+∠AOC=45°+30°=75°,同理∠DFB=75°,
故选项D正确.
∴∠AEO=∠BFO,
在△AOE和△BOF中,∠AEO=∠BFO,∠AOC=∠BOD,AO=BO,
∴△AOE≌△BOF,
∴OE=OF,
∴EC=FD,故选项C正确.
在△AOC中,∵OA=OC,∴∠ACO=∠CAO=![]() (180°-30°)=75°,
(180°-30°)=75°,
∴∠ACO=∠AEC,
∴AC=AE,同理BF=BD,
又∵AC=CD=BD,
∴CD=AE=BF,
∵在△OCD中,OE=OF,OC=OD,
∴EF<CD,
∴CD=AE=BF>EF,故A错误.
故选A.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】定义:将函数C的图象绕点P(0,n)旋转180°,得到新的函数C1的图象,我们称函数C1是函数C关于点P的相关函数.
例如:当n=1时,函数![]() 关于点P(0,1)的相关函数为
关于点P(0,1)的相关函数为![]() .
.
(1)当n=0时,
①二次函数y=x2关于点P的相关函数为 ;
②点A(2,3)在二次函数y=ax2﹣2ax+a(a≠0)关于点P的相关函数的图象上,求a的值;
(2)函数![]() 关于点P的相关函数是
关于点P的相关函数是![]() ,则n= ;
,则n= ;
(3)当![]() n﹣1≤x≤
n﹣1≤x≤![]() n+3时,函数
n+3时,函数![]() 的相关函数的最小值为7,求n的值.
的相关函数的最小值为7,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度.在同一时刻的阳光下,他们合作完成了以下工作:
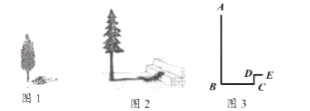
①测得一根长为l米的竹竿的影长为0.8米,甲树的影长为4.08米(如图l).
②测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米.
(1)在横线上直接填写甲树的高度为_____________米.
(2)图3为图2的示意图,请利用图3求出乙树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上点,点
是抛物线上点,点![]() 为射线
为射线![]() 上点(不含
上点(不含![]() 两点),且
两点),且![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 及抛物线解析式;
及抛物线解析式;
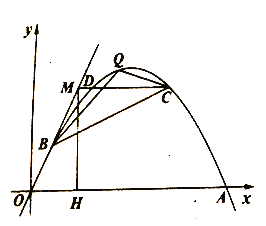
(2)如图,过点![]() 作
作![]() 轴,且与抛物线交于
轴,且与抛物线交于![]() 两点(
两点(![]() 位于
位于![]() 左边),若
左边),若![]() ,点
,点![]() 为直线
为直线![]() 上方的抛物线上点,求
上方的抛物线上点,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
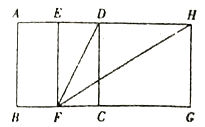
A. 矩形ABFE B. 矩形EFCD C. 矩形EFGH D. 矩形DCGH
查看答案和解析>>
科目:初中数学 来源: 题型:
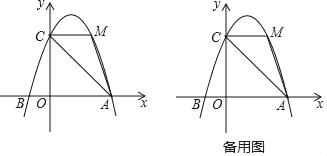
【题目】如图,已知抛物线过点A(3,0),B(﹣1,0),C(0,3),连接AC,点M是抛物线AC段上的一点,且CM∥x轴.
(1)求抛物线的解析式;
(2)求∠CAM的正切值;
(3)点Q在抛物线上,且∠BAQ=∠CAM,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com