
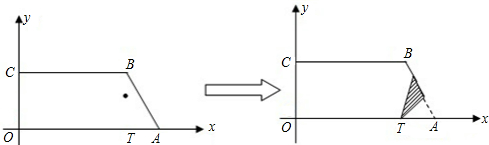
已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,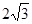 ),C(0,
),C(0,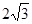 ),点T在线段OA上(不与线段端点重合),将纸片沿过T点的直线折叠,使点A落在射线AB上(记为点A′),折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片沿过T点的直线折叠,使点A落在射线AB上(记为点A′),折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;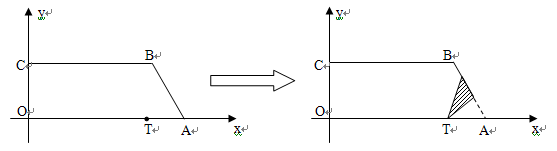
【小题1】(1)直接写出∠OAB的度数;
【小题2】(2)当纸片重叠部分的图形是四边形时,直接写出t的取值范围;
【小题3】(3)求S关于t的解析式及S的最大值.

【小题1】(1)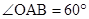
【小题2】(2) t的取值范围: 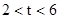 ...…………………………………………......2
...…………………………………………......2
【小题3】(3) ①当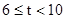 时,
时,
即当点A´在线段AB上时,
∵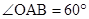 ,TA=TA´,
,TA=TA´,
∴△A´TA是等边三角形,且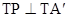 ,
,
∴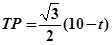 ,
, 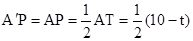 ,
,
∴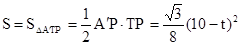 ,
,
当A´与B重合时,AT=AB=4,
∴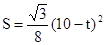 ,此时
,此时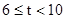 .
.
在对称轴t=10的左边,S的值随着t的
增大而减小,
∴当t=6时,S的值最大是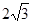 . .................................4’
. .................................4’
②当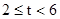 时,
时,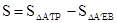
∵△A´EB的高是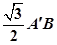 ,
,
∴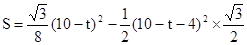
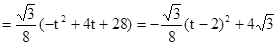
当t=2时,S的值最大是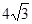 ; ......................................................6’
; ......................................................6’
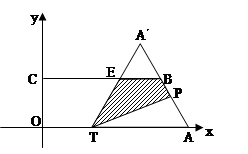
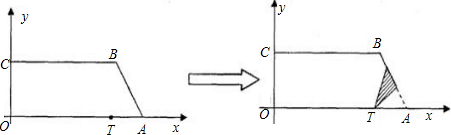
③当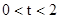 ,即当点A´和点P都在线
,即当点A´和点P都在线
段AB的延长线是(如图2,其中E是TA´
与CB的交点,F是TP与CB的交点),
∵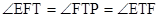 ,
,
四边形ETAB是等腰形,
∴EF=ET=AB=4,
∴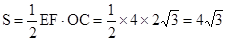
综上所述,S的最大值是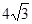 . ........................................................8
. ........................................................8
解析


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com