
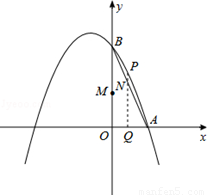
如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
解:(1)根据题意,设抛物线的解析式为: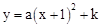 ,
,
∵点A(1,0),B(0,3)在抛物线上,
∴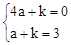 ,解得:
,解得: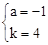 。
。
∴抛物线的解析式为: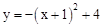 。
。
(2)①∵四边形OMPQ为矩形,
∴OM=PQ,即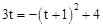 ,整理得:t2+5t﹣3=0,
,整理得:t2+5t﹣3=0,
解得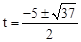 (
(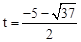 <0,舍去)。
<0,舍去)。
∴当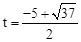 秒时,四边形OMPQ为矩形。
秒时,四边形OMPQ为矩形。
②Rt△AOB中,OA=1,OB=3,∴tanA=3。
若△AON为等腰三角形,有三种情况:
(I)若ON=AN,如答图1所示,
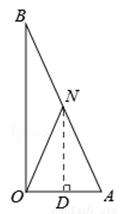
过点N作ND⊥OA于点D,
则D为OA中点,OD=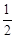 OA=
OA=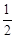 ,
,
∴t=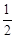 。
。
(II)若ON=OA,如答图2所示,
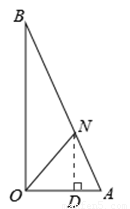
过点N作ND⊥OA于点D,
设AD=x,则ND=AD•tanA=3x,OD=OA﹣AD=1﹣x,
在Rt△NOD中,由勾股定理得:OD2+ND2=ON2,
即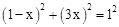 ,解得x1=
,解得x1=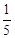 ,x2=0(舍去)。
,x2=0(舍去)。
∴x=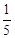 ,OD=1﹣x=
,OD=1﹣x=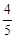 。
。
∴t=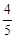 。
。
(III)若OA=AN,如答图3所示,
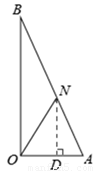
过点N作ND⊥OA于点D,
设AD=x,则ND=AD•tanA=3x,
在Rt△AND中,由勾股定理得:ND2+AD2=AN2,
即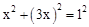 ,解得x1=
,解得x1=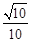 ,x2=
,x2=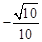 (舍去)。
(舍去)。
∴x=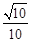 ,OD=1﹣x=1﹣
,OD=1﹣x=1﹣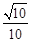 。
。
∴t=1﹣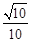 。
。
综上所述,当t为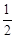 秒、
秒、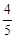 秒,1﹣
秒,1﹣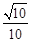 秒时,△AON为等腰三角形。
秒时,△AON为等腰三角形。
【解析】(1)用待定系数法求出抛物线的顶点式解析式。
(2)①当四边形OMPQ为矩形时,满足条件OM=PQ,据此列一元二次方程求解。
②△AON为等腰三角形时,可能存在三种情形,分类讨论,逐一计算。


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
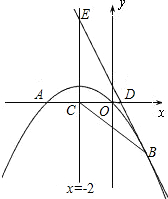 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,查看答案和解析>>
科目:初中数学 来源: 题型:
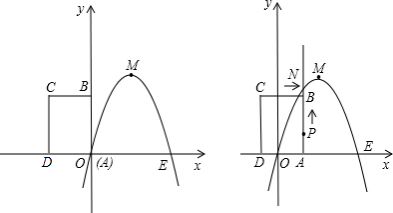
 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com